Question Number 118777 by obaidullah last updated on 19/Oct/20
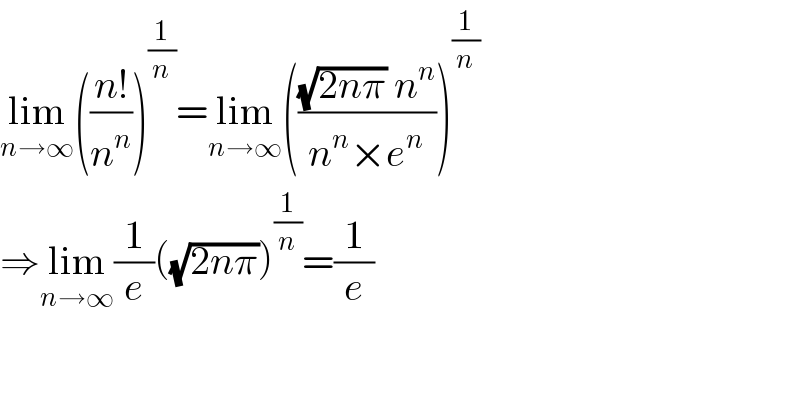
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{n}!}{{n}^{{n}} }\right)^{\frac{\mathrm{1}}{{n}}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\sqrt{\mathrm{2}{n}\pi}\:{n}^{{n}} }{{n}^{{n}} ×{e}^{{n}} }\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{e}}\left(\sqrt{\mathrm{2}{n}\pi}\right)^{\frac{\mathrm{1}}{{n}}} =\frac{\mathrm{1}}{{e}} \\ $$
Answered by mathmax by abdo last updated on 19/Oct/20

$$\mathrm{where}\:\mathrm{is}\:\mathrm{the}\:\mathrm{Question}? \\ $$
