Question Number 156993 by amin96 last updated on 18/Oct/21

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{n}} {\underbrace{\left({sin}\left({sin}\left({sin}\ldots\left({sin}\left({x}\right)\right)\ldots\right)}}\:\sqrt{{n}}=?\right.\right. \\ $$$$\mathrm{0}<{x}<\pi \\ $$
Commented by MathSh last updated on 18/Oct/21
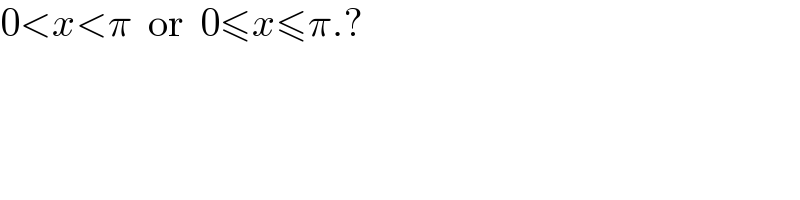
$$\mathrm{0}<{x}<\pi\:\:\mathrm{or}\:\:\mathrm{0}\leqslant{x}\leqslant\pi.? \\ $$
Commented by amin96 last updated on 18/Oct/21

$${no}\:\:\:\mathrm{0}<{x}<\pi \\ $$
Commented by MathSh last updated on 18/Oct/21
![a_x =lim_(n→∞) f_n (x) → a_x =sina_x → a_x =0 f_n (x)∼αn^(-r) f_(n+1) =sin f_n =f_n -((1/6))f_n ^3 +O(f_n ^5 ) αn^(-r) (1+(1/n))^(-r) ∼ αn^(-r) [1-((1/6))(αn^(-r) )^2 +O(n^(-4r) )] -rn^(-1) = - (α^2 /6) n^(-2r) α = (√3) → r = (1/2) ⇒lim_(n→∞) n^r f_n (x) = α = (√3) •](https://www.tinkutara.com/question/Q157005.png)
$$\mathrm{a}_{\boldsymbol{\mathrm{x}}} =\underset{\boldsymbol{\mathrm{n}}\rightarrow\infty} {\mathrm{lim}f}_{\boldsymbol{\mathrm{n}}} \left(\mathrm{x}\right)\:\rightarrow\:\mathrm{a}_{\boldsymbol{\mathrm{x}}} =\mathrm{sina}_{\boldsymbol{\mathrm{x}}} \:\rightarrow\:\mathrm{a}_{\boldsymbol{\mathrm{x}}} =\mathrm{0} \\ $$$$\mathrm{f}_{\boldsymbol{\mathrm{n}}} \left(\mathrm{x}\right)\sim\alpha\mathrm{n}^{-\boldsymbol{\mathrm{r}}} \\ $$$$\mathrm{f}_{\boldsymbol{\mathrm{n}}+\mathrm{1}} =\mathrm{sin}\:\mathrm{f}_{\boldsymbol{\mathrm{n}}} =\mathrm{f}_{\boldsymbol{\mathrm{n}}} -\left(\frac{\mathrm{1}}{\mathrm{6}}\right)\mathrm{f}_{\boldsymbol{\mathrm{n}}} ^{\mathrm{3}} +\mathrm{O}\left(\mathrm{f}_{\boldsymbol{\mathrm{n}}} ^{\mathrm{5}} \right) \\ $$$$\alpha\mathrm{n}^{-\boldsymbol{\mathrm{r}}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)^{-\boldsymbol{\mathrm{r}}} \sim\:\alpha\mathrm{n}^{-\boldsymbol{\mathrm{r}}} \left[\mathrm{1}-\left(\frac{\mathrm{1}}{\mathrm{6}}\right)\left(\alpha\mathrm{n}^{-\boldsymbol{\mathrm{r}}} \right)^{\mathrm{2}} +\mathrm{O}\left(\mathrm{n}^{-\mathrm{4}\boldsymbol{\mathrm{r}}} \right)\right] \\ $$$$-\mathrm{rn}^{-\mathrm{1}} =\:-\:\frac{\alpha^{\mathrm{2}} }{\mathrm{6}}\:\mathrm{n}^{-\mathrm{2}\boldsymbol{\mathrm{r}}} \\ $$$$\alpha\:=\:\sqrt{\mathrm{3}}\:\rightarrow\:\mathrm{r}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\underset{\boldsymbol{\mathrm{n}}\rightarrow\infty} {\mathrm{lim}n}^{\boldsymbol{\mathrm{r}}} \:\mathrm{f}_{\boldsymbol{\mathrm{n}}} \left(\mathrm{x}\right)\:=\:\alpha\:=\:\sqrt{\mathrm{3}}\:\bullet \\ $$
