Menu Close

lim-n-tan-pi-2n-tan-2pi-2n-tan-3pi-2n-tan-npi-2n-1-n-

Tinku Tara 0 Comments
Pin




Question Number 117078 by bemath last updated on 09/Oct/20
lim_(n→∞) [ tan ((π/(2n))).tan (((2π)/(2n))).tan (((3π)/(2n)))...tan (((nπ)/(2n)))]^(1/n) =?
$$\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\left[\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2n}}\right).\mathrm{tan}\:\left(\frac{\mathrm{2}\pi}{\mathrm{2n}}\right).\mathrm{tan}\:\left(\frac{\mathrm{3}\pi}{\mathrm{2n}}\right)…\mathrm{tan}\:\left(\frac{\mathrm{n}\pi}{\mathrm{2n}}\right)\right]^{\frac{\mathrm{1}}{\mathrm{n}}} =?\: \\ $$
Answered by Dwaipayan Shikari last updated on 09/Oct/20
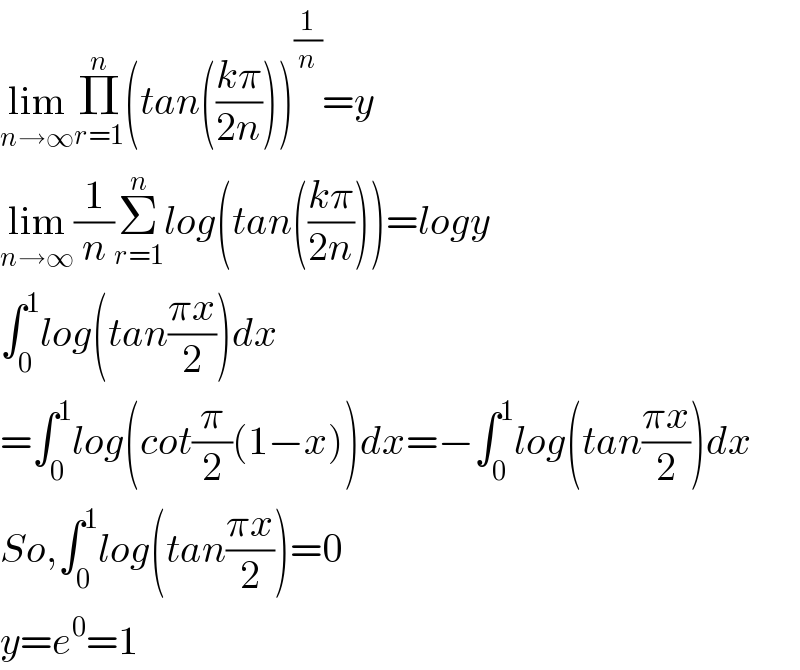
lim_(n→∞) Π_(r=1) ^n (tan(((kπ)/(2n))))^(1/n) =y lim_(n→∞) (1/n)Σ_(r=1) ^n log(tan(((kπ)/(2n))))=logy ∫_0 ^1 log(tan((πx)/2))dx =∫_0 ^1 log(cot(π/2)(1−x))dx=−∫_0 ^1 log(tan((πx)/2))dx So,∫_0 ^1 log(tan((πx)/2))=0 y=e^0 =1
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{r}=\mathrm{1}} {\overset{{n}} {\prod}}\left({tan}\left(\frac{{k}\pi}{\mathrm{2}{n}}\right)\right)^{\frac{\mathrm{1}}{{n}}} ={y} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{log}\left({tan}\left(\frac{{k}\pi}{\mathrm{2}{n}}\right)\right)={logy} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left({tan}\frac{\pi{x}}{\mathrm{2}}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left({cot}\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−{x}\right)\right){dx}=−\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left({tan}\frac{\pi{x}}{\mathrm{2}}\right){dx} \\ $$$${So},\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left({tan}\frac{\pi{x}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$${y}={e}^{\mathrm{0}} =\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *