Question Number 85708 by Roland Mbunwe last updated on 24/Mar/20
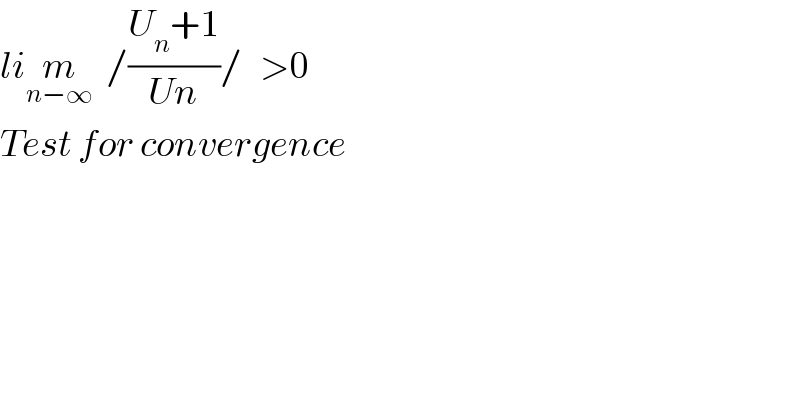
$${li}\underset{{n}−\infty} {{m}}\:\:/\frac{{U}_{{n}} +\mathrm{1}}{{Un}}/\:\:\:>\mathrm{0} \\ $$$${Test}\:{for}\:{convergence} \\ $$
Answered by Rio Michael last updated on 24/Mar/20

$$\mathrm{test}\:\mathrm{for}\:\mathrm{convergence}\:\mathrm{states}\:\mathrm{that} \\ $$$$\:\mathrm{if}\:{U}_{{n}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{sequence}\:\mathrm{and} \\ $$$$\:\bullet\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mid\frac{{U}_{{n}+\mathrm{1}} }{{U}_{{n}} }\mid\:>\:\mathrm{1}\:\:\Rightarrow\:{U}_{{n}} \:\mathrm{is}\:\mathrm{divergent}. \\ $$$$\bullet\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mid\frac{{U}_{{n}+\mathrm{1}} }{{U}_{{n}} }\mid\:<\:\mathrm{1}\:\Rightarrow\:{U}_{{n}} \:\mathrm{is}\:\mathrm{convergent}. \\ $$$$\bullet\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mid\frac{{U}_{{n}+\mathrm{1}} }{{U}_{{n}} }\mid\:=\:\mathrm{1}\:\Rightarrow\:\mathrm{inconclusive} \\ $$
