Question Number 113576 by bemath last updated on 14/Sep/20
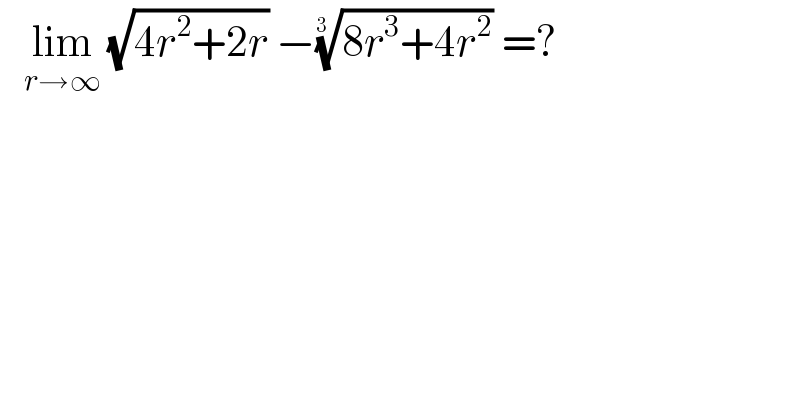
$$\:\:\:\underset{{r}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{4}{r}^{\mathrm{2}} +\mathrm{2}{r}}\:−\sqrt[{\mathrm{3}\:}]{\mathrm{8}{r}^{\mathrm{3}} +\mathrm{4}{r}^{\mathrm{2}} }\:=? \\ $$
Answered by bemath last updated on 14/Sep/20
![⇔ lim_(r→∞) r((√(4+(2/r)))−((8+(4/r)))^(1/(3 )) ) = [ set (1/r) = b , b→0] lim_(b→0) (((√(4+2b))−((8+4b))^(1/(3 )) )/b) = lim_(b→0) ((2(√(1+(b/2)))−2((1+(b/2)))^(1/(3 )) )/b) = 2×lim_(b→0) (((1+(b/4))−(1+(b/6)))/b) = 2×lim_(b→0) (((((3b−2b)/(12))))/b) = 2×(1/(12))=(1/6)](https://www.tinkutara.com/question/Q113579.png)
$$\Leftrightarrow\:\underset{{r}\rightarrow\infty} {\mathrm{lim}}{r}\left(\sqrt{\mathrm{4}+\frac{\mathrm{2}}{{r}}}−\sqrt[{\mathrm{3}\:}]{\mathrm{8}+\frac{\mathrm{4}}{{r}}}\right)\:= \\ $$$$\left[\:{set}\:\frac{\mathrm{1}}{{r}}\:=\:{b}\:,\:{b}\rightarrow\mathrm{0}\right] \\ $$$$\underset{{b}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{4}+\mathrm{2}{b}}−\sqrt[{\mathrm{3}\:}]{\mathrm{8}+\mathrm{4}{b}}}{{b}}\:= \\ $$$$\underset{{b}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\sqrt{\mathrm{1}+\frac{{b}}{\mathrm{2}}}−\mathrm{2}\sqrt[{\mathrm{3}\:}]{\mathrm{1}+\frac{{b}}{\mathrm{2}}}}{{b}}\:= \\ $$$$\mathrm{2}×\underset{{b}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\frac{{b}}{\mathrm{4}}\right)−\left(\mathrm{1}+\frac{{b}}{\mathrm{6}}\right)}{{b}}\:= \\ $$$$\mathrm{2}×\underset{{b}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\frac{\mathrm{3}{b}−\mathrm{2}{b}}{\mathrm{12}}\right)}{{b}}\:=\:\mathrm{2}×\frac{\mathrm{1}}{\mathrm{12}}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$
