Question Number 111383 by john santu last updated on 03/Sep/20
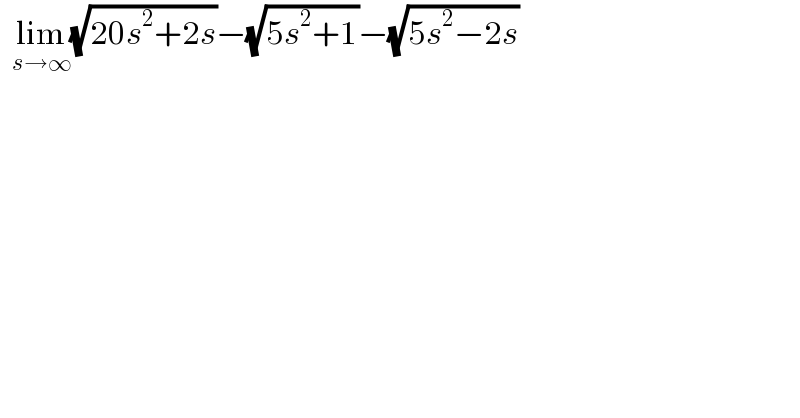
$$\:\:\underset{{s}\rightarrow\infty} {\mathrm{lim}}\sqrt{\mathrm{20}{s}^{\mathrm{2}} +\mathrm{2}{s}}−\sqrt{\mathrm{5}{s}^{\mathrm{2}} +\mathrm{1}}−\sqrt{\mathrm{5}{s}^{\mathrm{2}} −\mathrm{2}{s}} \\ $$
Answered by bobhans last updated on 03/Sep/20
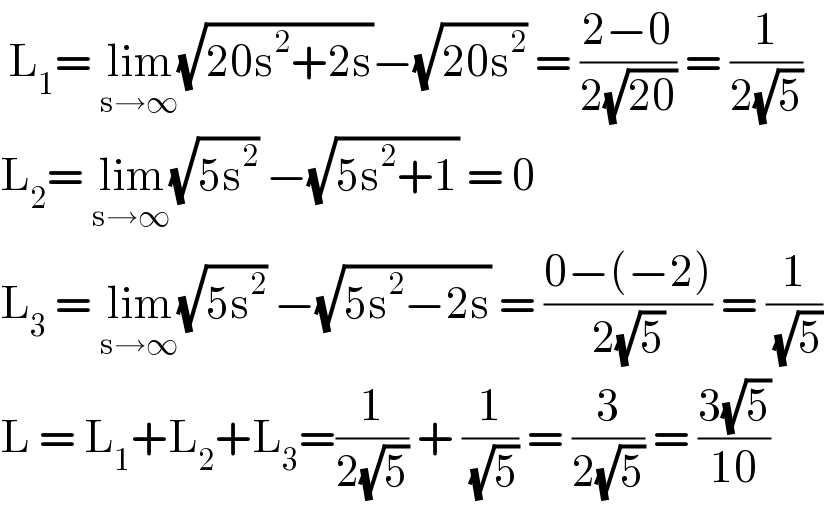
$$\:\mathrm{L}_{\mathrm{1}} =\:\underset{\mathrm{s}\rightarrow\infty} {\mathrm{lim}}\sqrt{\mathrm{20s}^{\mathrm{2}} +\mathrm{2s}}−\sqrt{\mathrm{20s}^{\mathrm{2}} }\:=\:\frac{\mathrm{2}−\mathrm{0}}{\mathrm{2}\sqrt{\mathrm{20}}}\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{5}}} \\ $$$$\mathrm{L}_{\mathrm{2}} =\:\underset{\mathrm{s}\rightarrow\infty} {\mathrm{lim}}\sqrt{\mathrm{5s}^{\mathrm{2}} }\:−\sqrt{\mathrm{5s}^{\mathrm{2}} +\mathrm{1}}\:=\:\mathrm{0} \\ $$$$\mathrm{L}_{\mathrm{3}} \:=\:\underset{\mathrm{s}\rightarrow\infty} {\mathrm{lim}}\sqrt{\mathrm{5s}^{\mathrm{2}} }\:−\sqrt{\mathrm{5s}^{\mathrm{2}} −\mathrm{2s}}\:=\:\frac{\mathrm{0}−\left(−\mathrm{2}\right)}{\mathrm{2}\sqrt{\mathrm{5}}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\mathrm{L}\:=\:\mathrm{L}_{\mathrm{1}} +\mathrm{L}_{\mathrm{2}} +\mathrm{L}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{5}}}\:+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\:=\:\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{5}}}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{10}} \\ $$
