Question Number 169743 by naka3546 last updated on 07/May/22
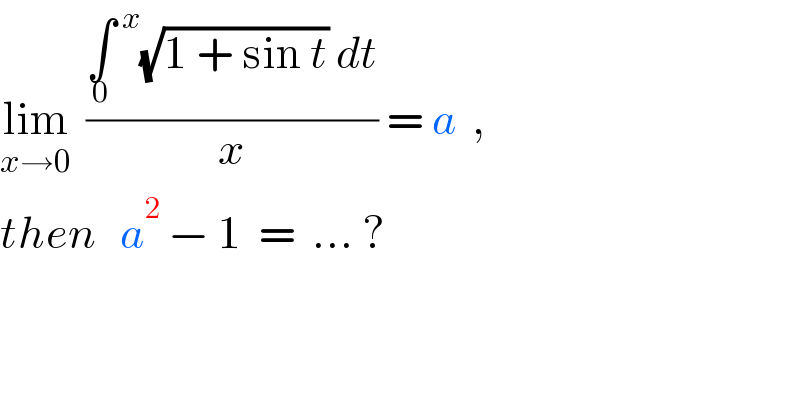
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\underset{\mathrm{0}} {\int}\overset{\:{x}} {\:}\sqrt{\mathrm{1}\:+\:\mathrm{sin}\:{t}}\:{dt}}{{x}}\:=\:{a}\:\:,\:\: \\ $$$${then}\:\:\:{a}^{\mathrm{2}} \:−\:\mathrm{1}\:\:=\:\:…\:? \\ $$
Answered by Mathspace last updated on 07/May/22
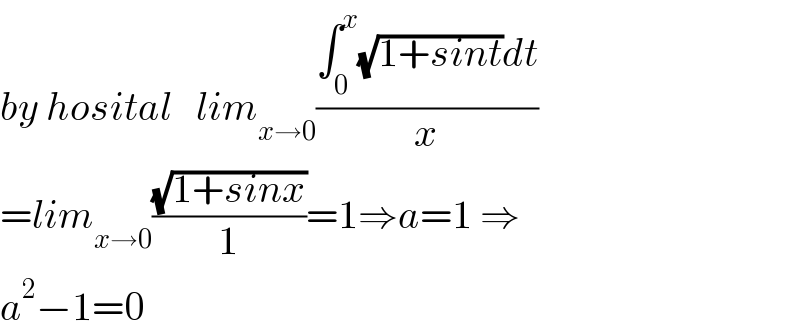
$${by}\:{hosital}\:\:\:{lim}_{{x}\rightarrow\mathrm{0}} \frac{\int_{\mathrm{0}} ^{{x}} \sqrt{\mathrm{1}+{sint}}{dt}}{{x}} \\ $$$$={lim}_{{x}\rightarrow\mathrm{0}} \frac{\sqrt{\mathrm{1}+{sinx}}}{\mathrm{1}}=\mathrm{1}\Rightarrow{a}=\mathrm{1}\:\Rightarrow \\ $$$${a}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$
Commented by naka3546 last updated on 07/May/22
$$\mathrm{Thank}\:\:\mathrm{you},\:\:{sir}\:. \\ $$
Answered by cortano1 last updated on 08/May/22
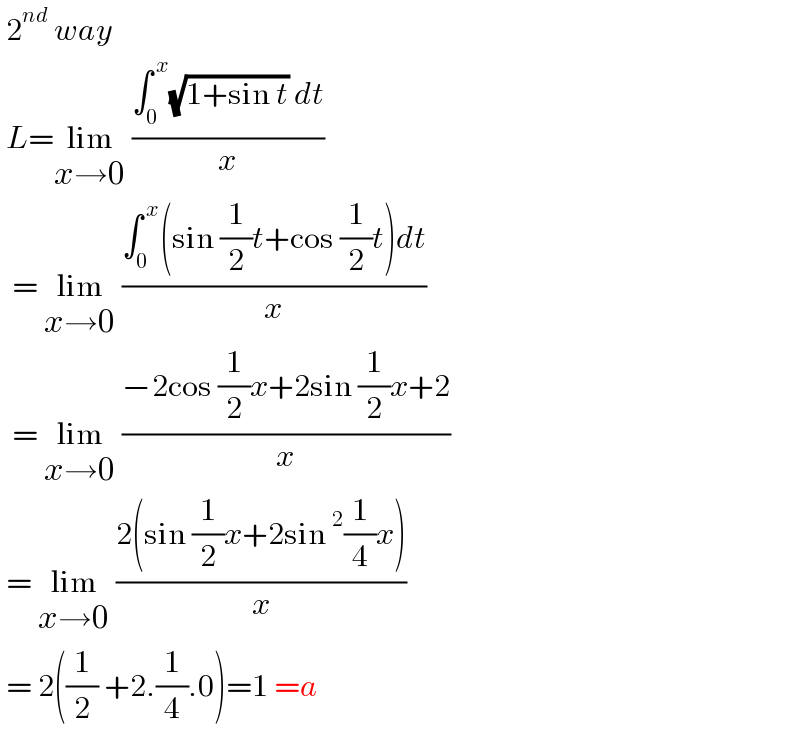
$$\:\mathrm{2}^{{nd}} \:{way} \\ $$$$\:{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\int_{\mathrm{0}} ^{\:{x}} \sqrt{\mathrm{1}+\mathrm{sin}\:{t}}\:{dt}}{{x}} \\ $$$$\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\int_{\mathrm{0}} ^{\:{x}} \left(\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}{t}+\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}{t}\right){dt}}{{x}} \\ $$$$\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2cos}\:\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{2sin}\:\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{2}}{{x}} \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\left(\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{2sin}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{4}}{x}\right)}{{x}} \\ $$$$\:=\:\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\:+\mathrm{2}.\frac{\mathrm{1}}{\mathrm{4}}.\mathrm{0}\right)=\mathrm{1}\:={a}\: \\ $$
