Question Number 94723 by john santu last updated on 20/May/20
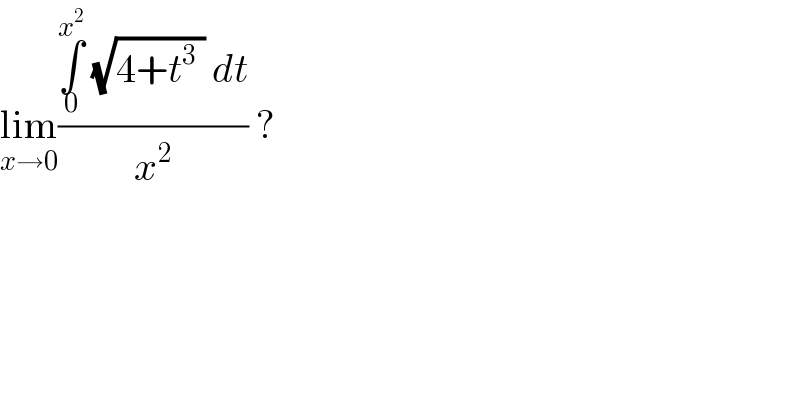
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\underset{\mathrm{0}} {\overset{{x}^{\mathrm{2}} } {\int}}\:\sqrt{\mathrm{4}+{t}^{\mathrm{3}} \:}\:{dt}}{{x}^{\mathrm{2}} }\:?\: \\ $$
Answered by i jagooll last updated on 20/May/20
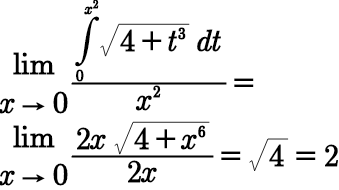
Answered by mathmax by abdo last updated on 20/May/20
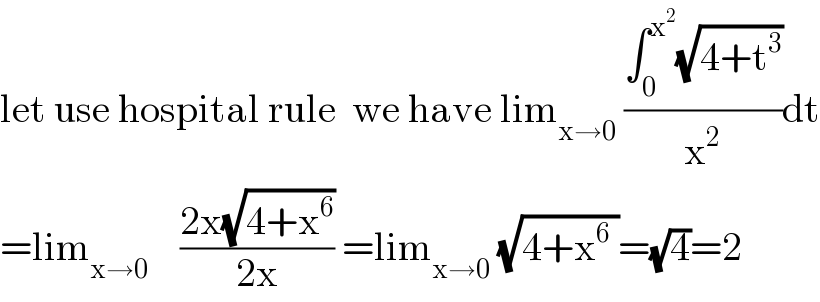
$$\mathrm{let}\:\mathrm{use}\:\mathrm{hospital}\:\mathrm{rule}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\frac{\int_{\mathrm{0}} ^{\mathrm{x}^{\mathrm{2}} } \sqrt{\mathrm{4}+\mathrm{t}^{\mathrm{3}} }}{\mathrm{x}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\:\:\frac{\mathrm{2x}\sqrt{\mathrm{4}+\mathrm{x}^{\mathrm{6}} }}{\mathrm{2x}}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\sqrt{\mathrm{4}+\mathrm{x}^{\mathrm{6}} \:}=\sqrt{\mathrm{4}}=\mathrm{2} \\ $$
