Question Number 93146 by i jagooll last updated on 11/May/20
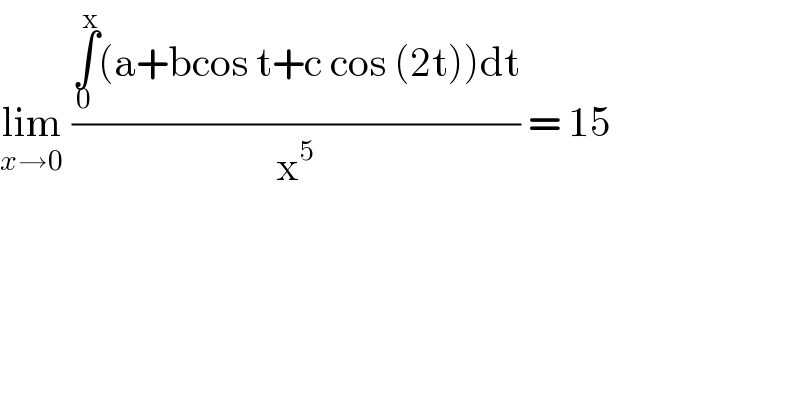
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\underset{\mathrm{0}} {\overset{\mathrm{x}} {\int}}\left(\mathrm{a}+\mathrm{bcos}\:\mathrm{t}+\mathrm{c}\:\mathrm{cos}\:\left(\mathrm{2t}\right)\right)\mathrm{dt}}{\mathrm{x}^{\mathrm{5}} }\:=\:\mathrm{15} \\ $$
Commented by i jagooll last updated on 11/May/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by john santu last updated on 11/May/20
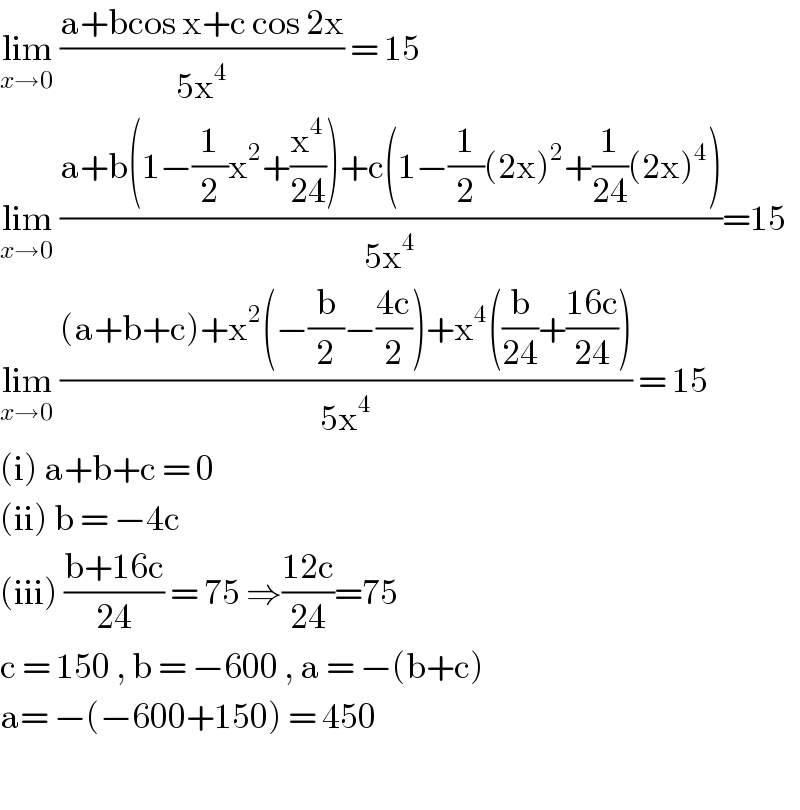
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{a}+\mathrm{bcos}\:\mathrm{x}+\mathrm{c}\:\mathrm{cos}\:\mathrm{2x}}{\mathrm{5x}^{\mathrm{4}} }\:=\:\mathrm{15}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{a}+\mathrm{b}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{24}}\right)+\mathrm{c}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2x}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{24}}\left(\mathrm{2x}\right)^{\mathrm{4}} \right)}{\mathrm{5x}^{\mathrm{4}} }=\mathrm{15} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)+\mathrm{x}^{\mathrm{2}} \left(−\frac{\mathrm{b}}{\mathrm{2}}−\frac{\mathrm{4c}}{\mathrm{2}}\right)+\mathrm{x}^{\mathrm{4}} \left(\frac{\mathrm{b}}{\mathrm{24}}+\frac{\mathrm{16c}}{\mathrm{24}}\right)}{\mathrm{5x}^{\mathrm{4}} }\:=\:\mathrm{15} \\ $$$$\left(\mathrm{i}\right)\:\mathrm{a}+\mathrm{b}+\mathrm{c}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{b}\:=\:−\mathrm{4c} \\ $$$$\left(\mathrm{iii}\right)\:\frac{\mathrm{b}+\mathrm{16c}}{\mathrm{24}}\:=\:\mathrm{75}\:\Rightarrow\frac{\mathrm{12c}}{\mathrm{24}}=\mathrm{75}\: \\ $$$$\mathrm{c}\:=\:\mathrm{150}\:,\:\mathrm{b}\:=\:−\mathrm{600}\:,\:\mathrm{a}\:=\:−\left(\mathrm{b}+\mathrm{c}\right) \\ $$$$\mathrm{a}=\:−\left(−\mathrm{600}+\mathrm{150}\right)\:=\:\mathrm{450} \\ $$$$ \\ $$
