Menu Close

lim-x-0-0-x-sin-2t-4-t-2-0-x-1-t-1-dt-dt-

Tinku Tara 0 Comments
Pin




Question Number 168964 by cortano1 last updated on 22/Apr/22
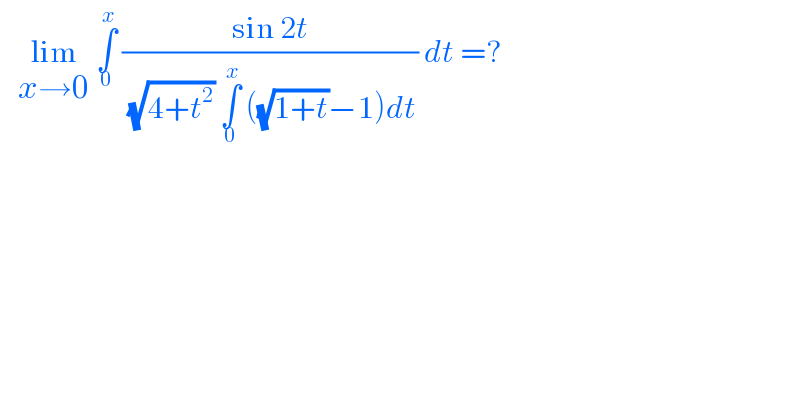
lim_(x→0) ∫_0 ^x ((sin 2t)/( (√(4+t^2 )) ∫_0 ^x ((√(1+t))−1)dt)) dt =?
$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\underset{\mathrm{0}} {\overset{{x}} {\int}}\:\frac{\mathrm{sin}\:\mathrm{2}{t}}{\:\sqrt{\mathrm{4}+{t}^{\mathrm{2}} }\:\underset{\mathrm{0}} {\overset{{x}} {\int}}\:\left(\sqrt{\mathrm{1}+{t}}−\mathrm{1}\right){dt}}\:{dt}\:=?\: \\ $$
Answered by greougoury555 last updated on 22/Apr/22
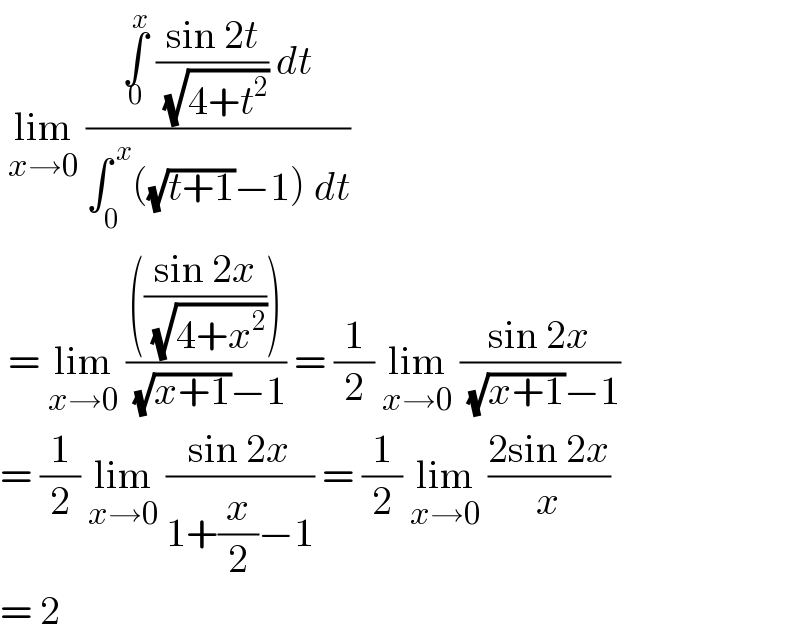
lim_(x→0) ((∫_0 ^x ((sin 2t)/( (√(4+t^2 )))) dt)/(∫_0 ^( x) ((√(t+1))−1) dt)) = lim_(x→0) (((((sin 2x)/( (√(4+x^2 ))))))/( (√(x+1))−1)) = (1/2) lim_(x→0) ((sin 2x)/( (√(x+1))−1)) = (1/2) lim_(x→0) ((sin 2x)/(1+(x/2)−1)) = (1/2) lim_(x→0) ((2sin 2x)/x) = 2
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\underset{\mathrm{0}} {\overset{{x}} {\int}}\:\frac{\mathrm{sin}\:\mathrm{2}{t}}{\:\sqrt{\mathrm{4}+{t}^{\mathrm{2}} }}\:{dt}}{\int_{\mathrm{0}} ^{\:{x}} \left(\sqrt{{t}+\mathrm{1}}−\mathrm{1}\right)\:{dt}} \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\frac{\mathrm{sin}\:\mathrm{2}{x}}{\:\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }}\right)}{\:\sqrt{{x}+\mathrm{1}}−\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{2}{x}}{\:\sqrt{{x}+\mathrm{1}}−\mathrm{1}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{1}+\frac{{x}}{\mathrm{2}}−\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2sin}\:\mathrm{2}{x}}{{x}} \\ $$$$=\:\mathrm{2}\: \\ $$
Answered by qaz last updated on 22/Apr/22
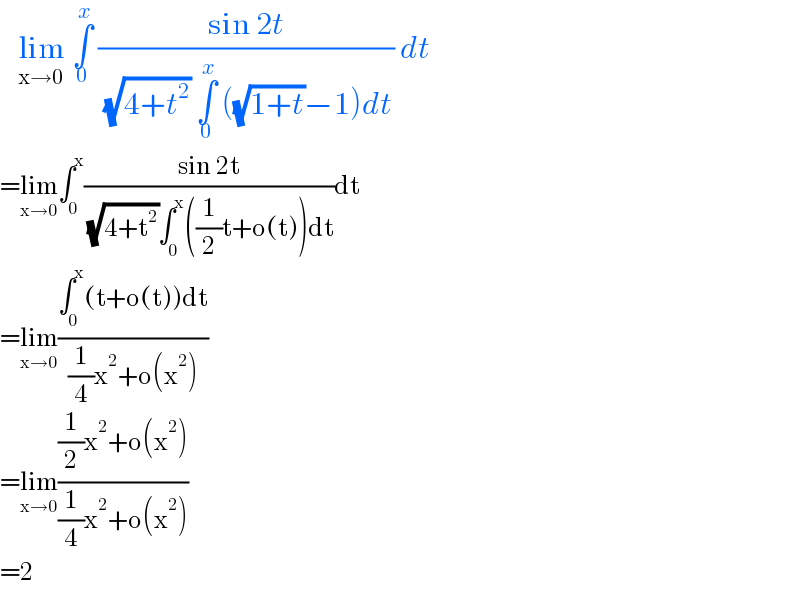
lim_(x→0) ∫_0 ^x ((sin 2t)/( (√(4+t^2 )) ∫_0 ^x ((√(1+t))−1)dt)) dt =lim_(x→0) ∫_0 ^x ((sin 2t)/( (√(4+t^2 ))∫_0 ^x ((1/2)t+o(t))dt))dt =lim_(x→0) ((∫_0 ^x (t+o(t))dt)/((1/4)x^2 +o(x^2 ))) =lim_(x→0) (((1/2)x^2 +o(x^2 ))/((1/4)x^2 +o(x^2 ))) =2
$$\:\:\:\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\underset{\mathrm{0}} {\overset{{x}} {\int}}\:\frac{\mathrm{sin}\:\mathrm{2}{t}}{\:\sqrt{\mathrm{4}+{t}^{\mathrm{2}} }\:\underset{\mathrm{0}} {\overset{{x}} {\int}}\:\left(\sqrt{\mathrm{1}+{t}}−\mathrm{1}\right){dt}}\:{dt}\: \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\int_{\mathrm{0}} ^{\mathrm{x}} \frac{\mathrm{sin}\:\mathrm{2t}}{\:\sqrt{\mathrm{4}+\mathrm{t}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{x}} \left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{t}+\mathrm{o}\left(\mathrm{t}\right)\right)\mathrm{dt}}\mathrm{dt} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\int_{\mathrm{0}} ^{\mathrm{x}} \left(\mathrm{t}+\mathrm{o}\left(\mathrm{t}\right)\right)\mathrm{dt}}{\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}^{\mathrm{2}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right)} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right)}{\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}^{\mathrm{2}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right)} \\ $$$$=\mathrm{2} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *