lim-x-0-1-1-1-x-1-1-1-x-x-

Question Number 171079 by greougoury555 last updated on 07/Jun/22

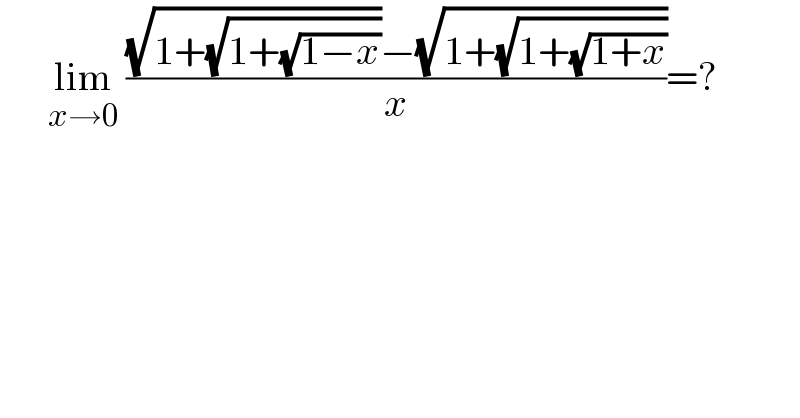
$$\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}−{x}}}}−\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+{x}}}}}{{x}}=? \\ $$

Commented by benhamimed last updated on 07/Jun/22

$$\frac{−\mathrm{1}}{\mathrm{24}} \\ $$

Commented by greougoury555 last updated on 08/Jun/22

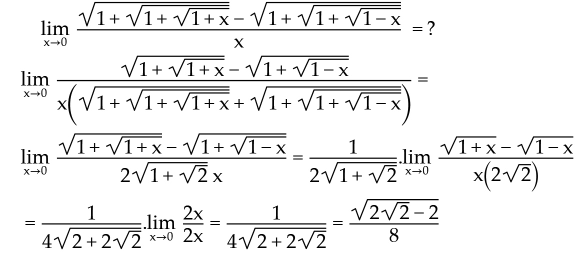
Answered by qaz last updated on 07/Jun/22

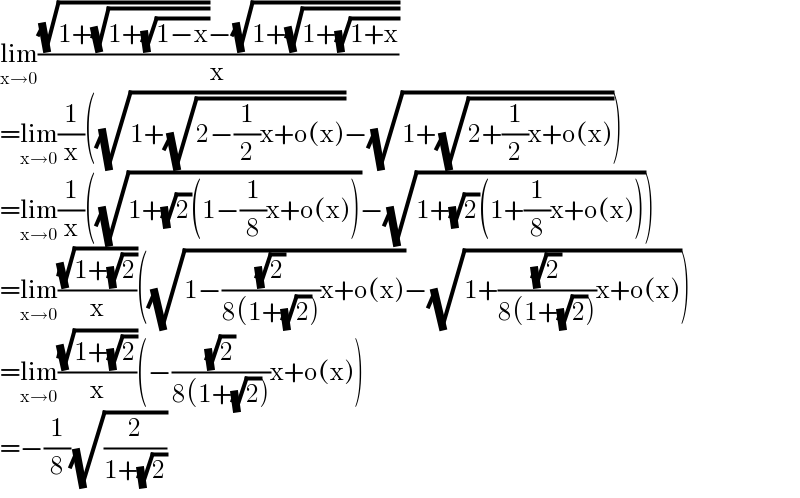
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{x}}}}−\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{x}}}}}{\mathrm{x}} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{x}}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}+\mathrm{o}\left(\mathrm{x}\right)}}−\sqrt{\mathrm{1}+\sqrt{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}+\mathrm{o}\left(\mathrm{x}\right)}}\right) \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{x}}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{x}+\mathrm{o}\left(\mathrm{x}\right)\right)}−\sqrt{\mathrm{1}+\sqrt{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{x}+\mathrm{o}\left(\mathrm{x}\right)\right)}\right) \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{1}+\sqrt{\mathrm{2}}}}{\mathrm{x}}\left(\sqrt{\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\mathrm{8}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}\mathrm{x}+\mathrm{o}\left(\mathrm{x}\right)}−\sqrt{\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{\mathrm{8}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}\mathrm{x}+\mathrm{o}\left(\mathrm{x}\right)}\right) \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{1}+\sqrt{\mathrm{2}}}}{\mathrm{x}}\left(−\frac{\sqrt{\mathrm{2}}}{\mathrm{8}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}\mathrm{x}+\mathrm{o}\left(\mathrm{x}\right)\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{8}}\sqrt{\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{2}}}} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com