Menu Close

lim-x-0-1-1-x-3-1-3-2-1-3-2x-3-

Tinku Tara 0 Comments
Pin




Question Number 78865 by jagoll last updated on 21/Jan/20
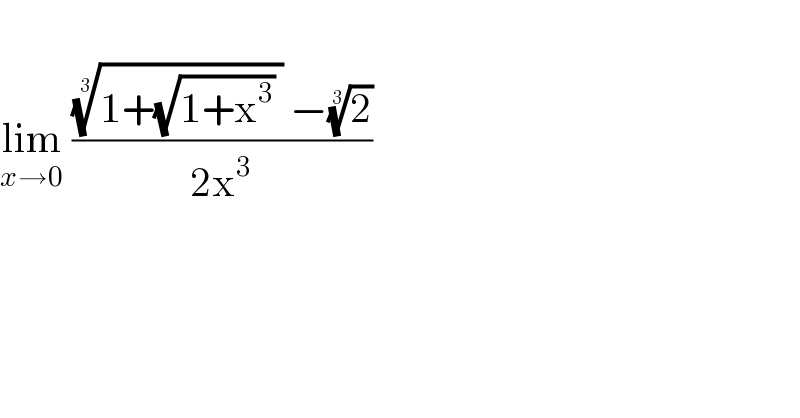
lim_(x→0) ((((1+(√(1+x^3 )) ))^(1/3) −(2)^(1/3) )/(2x^3 ))
$$ \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\:}\:−\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{2x}^{\mathrm{3}} } \\ $$
Commented by jagoll last updated on 21/Jan/20
dear mr Mjs . what value the limit? i′m got (1/(24)). my answer is correct?
$$\mathrm{dear}\:\mathrm{mr}\:\mathrm{Mjs}\:.\:\mathrm{what}\:\mathrm{value}\:\mathrm{the}\:\mathrm{limit}? \\ $$$$\mathrm{i}'\mathrm{m}\:\mathrm{got}\:\frac{\mathrm{1}}{\mathrm{24}}.\:\mathrm{my}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{correct}? \\ $$
Commented by john santu last updated on 21/Jan/20
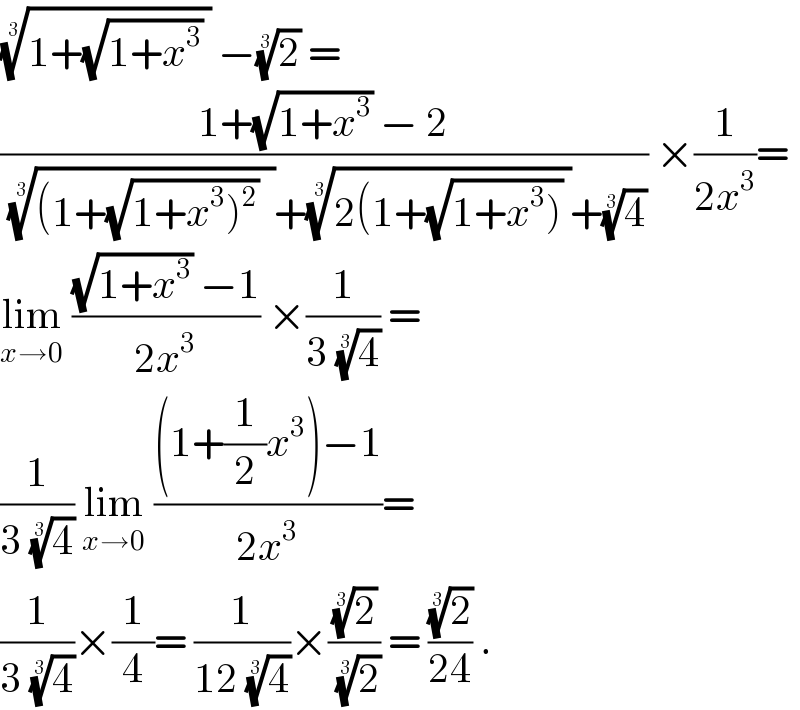
((1+(√(1+x^3 )) ))^(1/3) −(2)^(1/3) = ((1+(√(1+x^3 )) − 2)/( (((1+(√(1+x^3 )^2 )) ))^(1/3) +((2(1+(√(1+x^3 ))) ))^(1/3) +(4)^(1/3) )) ×(1/(2x^3 ))= lim_(x→0) (((√(1+x^3 )) −1)/(2x^3 )) ×(1/(3 (4)^(1/3) )) = (1/(3 (4)^(1/3) )) lim_(x→0) (((1+(1/2)x^3 )−1)/(2x^3 ))= (1/(3 (4)^(1/3) ))×(1/4)= (1/(12 (4)^(1/3) ))×((2)^(1/3) /( (2)^(1/3) )) = ((2)^(1/3) /(24)) .
$$\sqrt[{\mathrm{3}}]{\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }\:}\:−\sqrt[{\mathrm{3}}]{\mathrm{2}}\:=\: \\ $$$$\frac{\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }\:−\:\mathrm{2}}{\:\sqrt[{\mathrm{3}}]{\left(\mathrm{1}+\sqrt{\left.\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} }\:\:\right.}+\sqrt[{\mathrm{3}}]{\mathrm{2}\left(\mathrm{1}+\sqrt{\left.\mathrm{1}+{x}^{\mathrm{3}} \right)}\:\right.}+\sqrt[{\mathrm{3}}]{\mathrm{4}}}\:×\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{3}} }= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }\:−\mathrm{1}}{\mathrm{2}{x}^{\mathrm{3}} }\:×\frac{\mathrm{1}}{\mathrm{3}\:\sqrt[{\mathrm{3}}]{\mathrm{4}}}\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{3}\:\sqrt[{\mathrm{3}}]{\mathrm{4}}}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{3}} \right)−\mathrm{1}}{\mathrm{2}{x}^{\mathrm{3}} }= \\ $$$$\frac{\mathrm{1}}{\mathrm{3}\:\sqrt[{\mathrm{3}}]{\mathrm{4}}}×\frac{\mathrm{1}}{\mathrm{4}}=\:\frac{\mathrm{1}}{\mathrm{12}\:\sqrt[{\mathrm{3}}]{\mathrm{4}}}×\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}}\:=\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{24}}\:. \\ $$
Commented by john santu last updated on 21/Jan/20
wrong sir
$${wrong}\:{sir} \\ $$
Commented by jagoll last updated on 21/Jan/20
((2)^(1/3) /(24)) sir
$$\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{24}}\:\mathrm{sir} \\ $$
Commented by jagoll last updated on 21/Jan/20
yes sir. i agree.
$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{agree}. \\ $$
Answered by MJS last updated on 21/Jan/20
(((d/dx)[((1+(√(1+x^3 ))))^(1/3) −(2)^(1/3) ])/((d/dx)[2x^3 ]))=((x^2 /(2(√(1+x^3 ))(((1+(√(1+x^3 )))^2 ))^(1/3) ))/(6x^2 ))= =(1/(12(√(1+x^3 ))(((1+(√(1+x^3 )))^2 ))^(1/3) )) and the value of this with x=0 is ((2)^(1/3) /(24))
$$\frac{\frac{{d}}{{dx}}\left[\sqrt[{\mathrm{3}}]{\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }}−\sqrt[{\mathrm{3}}]{\mathrm{2}}\right]}{\frac{{d}}{{dx}}\left[\mathrm{2}{x}^{\mathrm{3}} \right]}=\frac{\frac{{x}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }\sqrt[{\mathrm{3}}]{\left(\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }\right)^{\mathrm{2}} }}}{\mathrm{6}{x}^{\mathrm{2}} }= \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }\sqrt[{\mathrm{3}}]{\left(\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }\right)^{\mathrm{2}} }} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{this}\:\mathrm{with}\:{x}=\mathrm{0}\:\mathrm{is}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{24}} \\ $$
Commented by jagoll last updated on 21/Jan/20
thanks sir
$$\mathrm{thanks}\:\mathrm{sir} \\ $$
Commented by Henri Boucatchou last updated on 21/Jan/20
Alright with Hospital Rule
$$\boldsymbol{{A}}{lright}\:{with}\:\:{Hospital}\:{Rule} \\ $$
Answered by behi83417@gmail.com last updated on 22/Jan/20
1+x^3 =t^2 [x→0⇒t→1] L=lim_(t→1) ((((1+t))^(1/3) −(2)^(1/3) )/(2(t^2 −1))) 1+t=r^3 [t→1⇒r→(2)^(1/3) ] L=lim_(r→(2)^(1/3) ) ((r−(2)^(1/3) )/(2[(r^3 −1)^2 −1]))=lim_(r→(2)^(1/3) ) (1/(2[6r^2 (r^3 −1)]))= =(1/(2×6(4)^(1/3) ))=((2)^(1/3) /(24))
$$\mathrm{1}+\mathrm{x}^{\mathrm{3}} =\mathrm{t}^{\mathrm{2}} \left[\mathrm{x}\rightarrow\mathrm{0}\Rightarrow\mathrm{t}\rightarrow\mathrm{1}\right] \\ $$$$\mathrm{L}=\underset{\mathrm{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{t}}−\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{2}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$$\mathrm{1}+\mathrm{t}=\mathrm{r}^{\mathrm{3}} \left[\mathrm{t}\rightarrow\mathrm{1}\Rightarrow\mathrm{r}\rightarrow\sqrt[{\mathrm{3}}]{\mathrm{2}}\right] \\ $$$$\mathrm{L}=\underset{\mathrm{r}\rightarrow\sqrt[{\mathrm{3}}]{\mathrm{2}}} {\mathrm{lim}}\frac{\mathrm{r}−\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{2}\left[\left(\mathrm{r}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\right]}=\underset{\mathrm{r}\rightarrow\sqrt[{\mathrm{3}}]{\mathrm{2}}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{2}\left[\mathrm{6r}^{\mathrm{2}} \left(\mathrm{r}^{\mathrm{3}} −\mathrm{1}\right)\right]}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}×\mathrm{6}\sqrt[{\mathrm{3}}]{\mathrm{4}}}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{24}} \\ $$
Commented by john santu last updated on 22/Jan/20
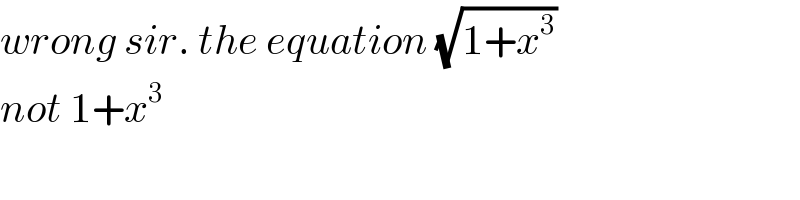
wrong sir. the equation (√(1+x^3 )) not 1+x^(3 )
$${wrong}\:{sir}.\:{the}\:{equation}\:\sqrt{\mathrm{1}+{x}^{\mathrm{3}} } \\ $$$${not}\:\mathrm{1}+{x}^{\mathrm{3}\:} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *