Question Number 113651 by bemath last updated on 14/Sep/20
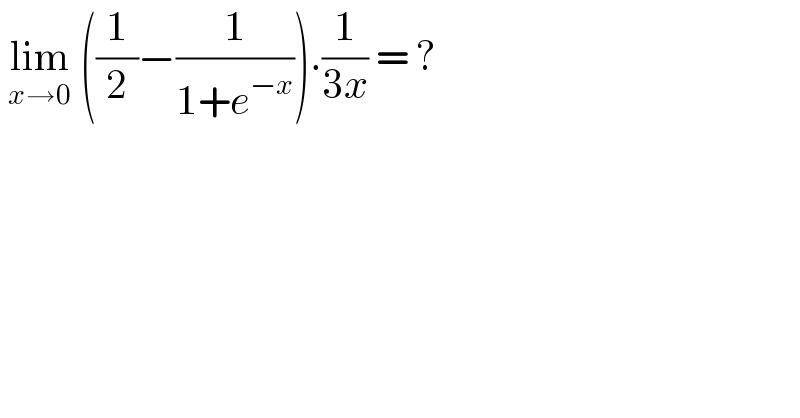
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{1}+{e}^{−{x}} }\right).\frac{\mathrm{1}}{\mathrm{3}{x}}\:=\:? \\ $$
Answered by john santu last updated on 14/Sep/20

$${by}\:{Taylor}\:{series}\: \\ $$$${let}\:{f}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}+{e}^{−{x}} }\:=\frac{\mathrm{1}}{\mathrm{2}}+\frac{{x}}{\mathrm{4}}−\frac{{x}^{\mathrm{3}} }{\mathrm{48}}+\frac{{x}^{\mathrm{5}} }{\mathrm{480}}−… \\ $$$${then}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{1}+{e}^{−{x}} }}{\mathrm{3}{x}}\:=\: \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{2}}−\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{{x}}{\mathrm{4}}−\frac{{x}^{\mathrm{3}} }{\mathrm{48}}+…\right)}{\mathrm{3}{x}}\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\frac{{x}}{\mathrm{4}}+\frac{{x}^{\mathrm{3}} }{\mathrm{48}}−…}{\mathrm{3}{x}}\:=\:−\frac{\mathrm{1}}{\mathrm{12}} \\ $$
Answered by bobhans last updated on 14/Sep/20
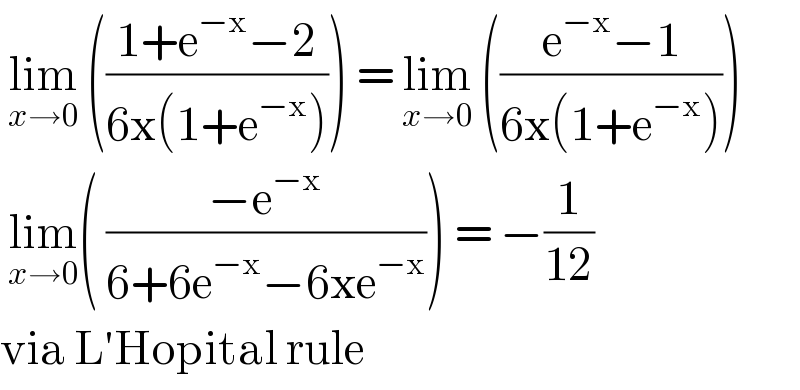
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} −\mathrm{2}}{\mathrm{6x}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{x}} \right)}\right)\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{e}^{−\mathrm{x}} −\mathrm{1}}{\mathrm{6x}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{x}} \right)}\right) \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\:\frac{−\mathrm{e}^{−\mathrm{x}} }{\mathrm{6}+\mathrm{6e}^{−\mathrm{x}} −\mathrm{6xe}^{−\mathrm{x}} }\right)\:=\:−\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$\mathrm{via}\:\mathrm{L}'\mathrm{Hopital}\:\mathrm{rule} \\ $$
Answered by Dwaipayan Shikari last updated on 14/Sep/20
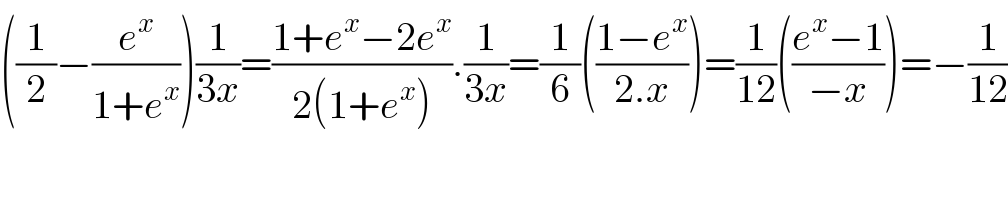
$$\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{{e}^{{x}} }{\mathrm{1}+{e}^{{x}} }\right)\frac{\mathrm{1}}{\mathrm{3}{x}}=\frac{\mathrm{1}+{e}^{{x}} −\mathrm{2}{e}^{{x}} }{\mathrm{2}\left(\mathrm{1}+{e}^{{x}} \right)}.\frac{\mathrm{1}}{\mathrm{3}{x}}=\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\mathrm{1}−{e}^{{x}} }{\mathrm{2}.{x}}\right)=\frac{\mathrm{1}}{\mathrm{12}}\left(\frac{{e}^{{x}} −\mathrm{1}}{−{x}}\right)=−\frac{\mathrm{1}}{\mathrm{12}} \\ $$
