Question Number 167028 by cortano1 last updated on 04/Mar/22
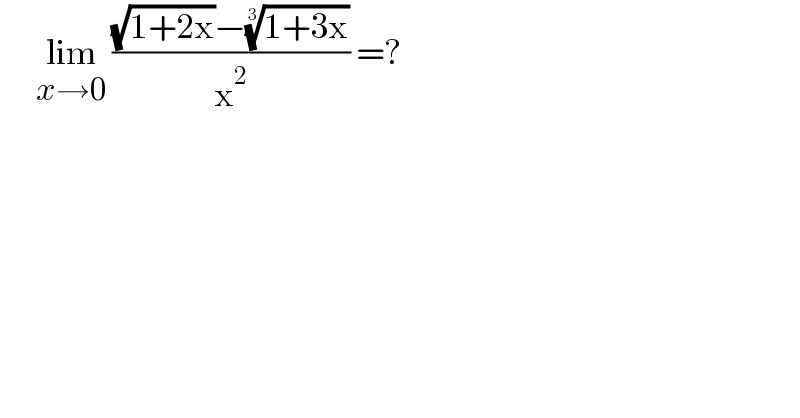
$$\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}+\mathrm{2x}}−\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{3x}}}{\mathrm{x}^{\mathrm{2}} }\:=? \\ $$
Answered by qaz last updated on 05/Mar/22
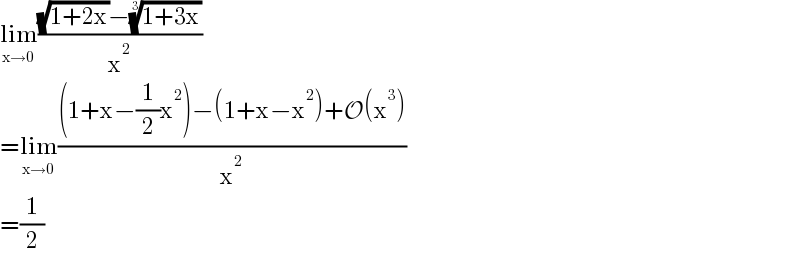
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{1}+\mathrm{2x}}−\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{3x}}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \right)−\left(\mathrm{1}+\mathrm{x}−\mathrm{x}^{\mathrm{2}} \right)+\mathcal{O}\left(\mathrm{x}^{\mathrm{3}} \right)}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
