Question Number 169052 by cortano1 last updated on 23/Apr/22
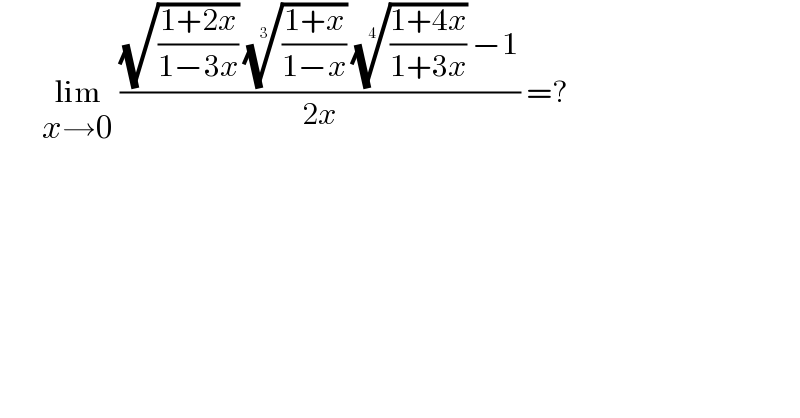
$$\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\frac{\mathrm{1}+\mathrm{2}{x}}{\mathrm{1}−\mathrm{3}{x}}}\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}\:\sqrt[{\mathrm{4}}]{\frac{\mathrm{1}+\mathrm{4}{x}}{\mathrm{1}+\mathrm{3}{x}}}\:−\mathrm{1}}{\mathrm{2}{x}}\:=? \\ $$
Commented by infinityaction last updated on 23/Apr/22

$$\frac{\mathrm{41}}{\mathrm{24}}??? \\ $$
Commented by cortano1 last updated on 23/Apr/22

$$\checkmark \\ $$
Commented by infinityaction last updated on 27/Apr/22

$${use}\:{binomial}\:{expansions} \\ $$$${binomial}\:{theorem}\:{for}\:{rational}\:{index} \\ $$$$\left(\mathrm{1}+{x}\right)^{{n}} \:=\:\mathrm{1}+{nx}+…\:\:\:\:{where}\:−\mathrm{1}<{x}<\mathrm{1} \\ $$$$\:\boldsymbol{{p}}\left(\boldsymbol{{let}}\right)=\:\underset{{x}\rightarrow\mathrm{0}} {\boldsymbol{\mathrm{lim}}}\:\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{x}}}\left\{\frac{\left(\mathrm{1}+\boldsymbol{{x}}\right)\left(\mathrm{1}+\frac{\boldsymbol{{x}}}{\mathrm{3}}\right)\left(\mathrm{1}+\boldsymbol{{x}}\right)}{\left(\mathrm{1}−\frac{\mathrm{3}\boldsymbol{{x}}}{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\boldsymbol{{x}}}{\mathrm{3}}\right)\left(\mathrm{1}+\frac{\mathrm{3}\boldsymbol{{x}}}{\mathrm{4}}\right)}−\mathrm{1}\right\} \\ $$$$\:\:{p}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{2}{x}}\left\{\frac{\left(\mathrm{1}+\boldsymbol{{x}}\right)^{\mathrm{2}} \left(\mathrm{3}+\boldsymbol{{x}}\right)/\mathrm{3}}{\left(\mathrm{2}−\mathrm{3}\boldsymbol{{x}}\right)\left(\mathrm{3}−\boldsymbol{{x}}\right)\left(\mathrm{4}+\mathrm{3}\boldsymbol{{x}}\right)/\mathrm{24}}−\mathrm{1}\right\} \\ $$$$\:\boldsymbol{{p}}=\underset{{x}\rightarrow\mathrm{0}} {\boldsymbol{\mathrm{lim}}}\:\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{x}}}\left\{\frac{\mathrm{8}\left(\mathrm{1}+\boldsymbol{{x}}\right)^{\mathrm{2}} \left(\mathrm{3}+\boldsymbol{{x}}\right)}{\left(\mathrm{2}−\mathrm{3}\boldsymbol{{x}}\right)\left(\mathrm{3}−\boldsymbol{{x}}\right)\left(\mathrm{4}+\mathrm{3}\boldsymbol{{x}}\right)}−\mathrm{1}\right\} \\ $$$$\:\:\:{p}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{1}}{\mathrm{2}{x}}\left\{\frac{\mathrm{8}\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \left(\mathrm{3}+{x}\right)−\left(\mathrm{2}−\mathrm{3}{x}\right)\left(\mathrm{3}−{x}\right)\left(\mathrm{4}+\mathrm{3}{x}\right)}{\left(\mathrm{2}−\mathrm{3}{x}\right)\left(\mathrm{3}−{x}\right)\left(\mathrm{4}+\mathrm{3}{x}\right)}\right\} \\ $$$$\:{p}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{2}{x}}\left\{\frac{\mathrm{8}{x}^{\mathrm{3}} +\mathrm{40}{x}^{\mathrm{2}} +\mathrm{56}{x}+\mathrm{24}−\mathrm{9}{x}^{\mathrm{3}} +\mathrm{21}{x}^{\mathrm{2}} +\mathrm{26}{x}−\mathrm{24}}{\left(\mathrm{2}−\mathrm{3}{x}\right)\left(\mathrm{3}−{x}\right)\left(\mathrm{4}+\mathrm{3}{x}\right)}\right\} \\ $$$$\:\:\boldsymbol{{p}}=\underset{{x}\rightarrow\mathrm{0}} {\boldsymbol{\mathrm{lim}}}\:\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{x}}}\left\{\frac{−\boldsymbol{{x}}^{\mathrm{3}} +\mathrm{61}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{82}\boldsymbol{{x}}}{\left(\mathrm{2}−\mathrm{3}\boldsymbol{{x}}\right)\left(\mathrm{3}−\boldsymbol{{x}}\right)\left(\mathrm{4}+\mathrm{3}\boldsymbol{{x}}\right)}\right\} \\ $$$$\:\:\boldsymbol{{p}}=\underset{{x}\rightarrow\mathrm{0}} {\boldsymbol{\mathrm{lim}}}\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{−\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{61}\boldsymbol{{x}}+\mathrm{82}}{\left(\mathrm{2}−\mathrm{3}\boldsymbol{{x}}\right)\left(\mathrm{3}−\boldsymbol{{x}}\right)\left(\mathrm{4}+\mathrm{3}\boldsymbol{{x}}\right)}\right\} \\ $$$$\:\:\:\:{p}=\:\:\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{82}}{\mathrm{24}} \\ $$$$\:\:\:\:{p}\:=\:\frac{\mathrm{41}}{\mathrm{24}} \\ $$$$ \\ $$
Answered by qaz last updated on 24/Apr/22
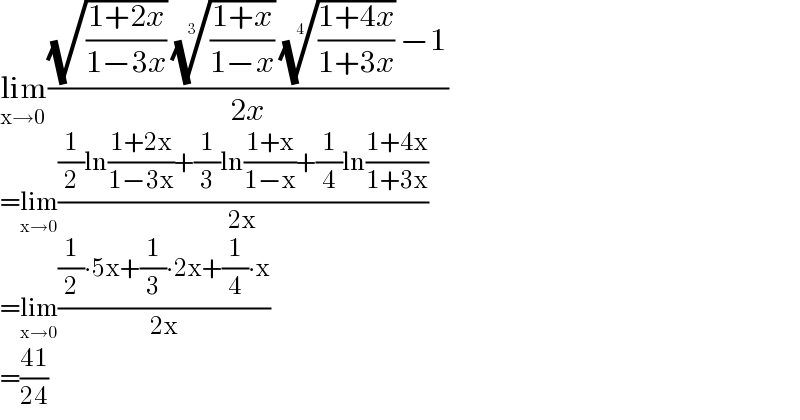
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\frac{\mathrm{1}+\mathrm{2}{x}}{\mathrm{1}−\mathrm{3}{x}}}\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}\:\sqrt[{\mathrm{4}}]{\frac{\mathrm{1}+\mathrm{4}{x}}{\mathrm{1}+\mathrm{3}{x}}}\:−\mathrm{1}}{\mathrm{2}{x}} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\frac{\mathrm{1}+\mathrm{2x}}{\mathrm{1}−\mathrm{3x}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\frac{\mathrm{1}+\mathrm{x}}{\mathrm{1}−\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\frac{\mathrm{1}+\mathrm{4x}}{\mathrm{1}+\mathrm{3x}}}{\mathrm{2x}} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}}\centerdot\mathrm{5x}+\frac{\mathrm{1}}{\mathrm{3}}\centerdot\mathrm{2x}+\frac{\mathrm{1}}{\mathrm{4}}\centerdot\mathrm{x}}{\mathrm{2x}} \\ $$$$=\frac{\mathrm{41}}{\mathrm{24}} \\ $$
Commented by infinityaction last updated on 24/Apr/22
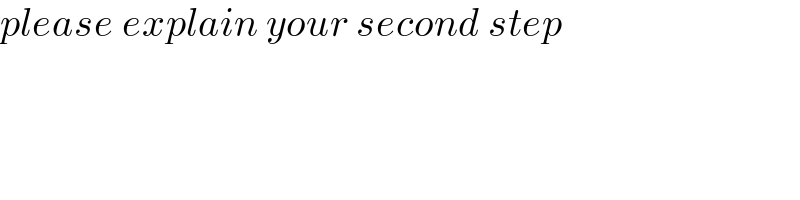
$${please}\:{explain}\:{your}\:{second}\:{step} \\ $$
Commented by qaz last updated on 24/Apr/22
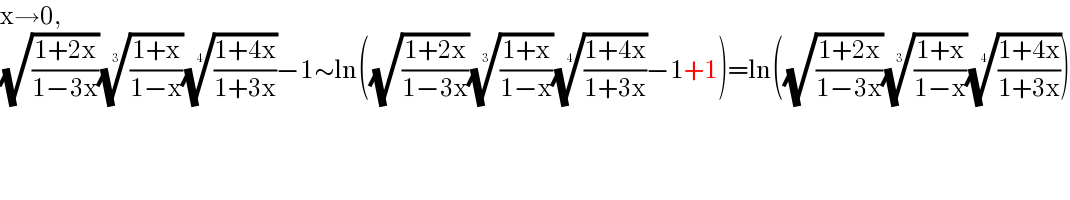
$$\mathrm{x}\rightarrow\mathrm{0}, \\ $$$$\sqrt{\frac{\mathrm{1}+\mathrm{2x}}{\mathrm{1}−\mathrm{3x}}}\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}+\mathrm{x}}{\mathrm{1}−\mathrm{x}}}\sqrt[{\mathrm{4}}]{\frac{\mathrm{1}+\mathrm{4x}}{\mathrm{1}+\mathrm{3x}}}−\mathrm{1}\sim\mathrm{ln}\left(\sqrt{\frac{\mathrm{1}+\mathrm{2x}}{\mathrm{1}−\mathrm{3x}}}\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}+\mathrm{x}}{\mathrm{1}−\mathrm{x}}}\sqrt[{\mathrm{4}}]{\frac{\mathrm{1}+\mathrm{4x}}{\mathrm{1}+\mathrm{3x}}}−\mathrm{1}+\mathrm{1}\right)=\mathrm{ln}\left(\sqrt{\frac{\mathrm{1}+\mathrm{2x}}{\mathrm{1}−\mathrm{3x}}}\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}+\mathrm{x}}{\mathrm{1}−\mathrm{x}}}\sqrt[{\mathrm{4}}]{\frac{\mathrm{1}+\mathrm{4x}}{\mathrm{1}+\mathrm{3x}}}\right) \\ $$
Commented by qaz last updated on 24/Apr/22
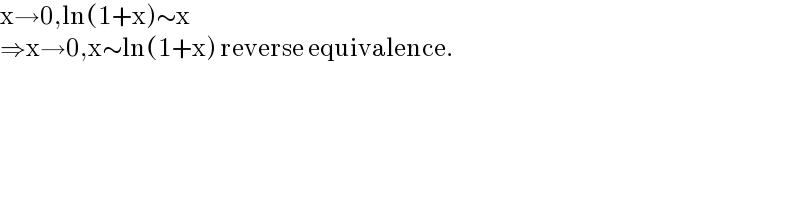
$$\mathrm{x}\rightarrow\mathrm{0},\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\sim\mathrm{x} \\ $$$$\Rightarrow\mathrm{x}\rightarrow\mathrm{0},\mathrm{x}\sim\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\:\mathrm{reverse}\:\mathrm{equivalence}. \\ $$
Commented by infinityaction last updated on 24/Apr/22
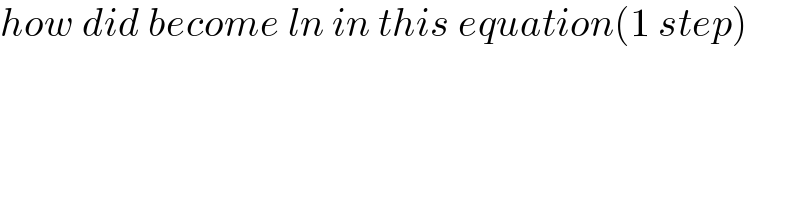
$${how}\:{did}\:{become}\:{ln}\:{in}\:{this}\:{equation}\left(\mathrm{1}\:{step}\right) \\ $$$$ \\ $$
Commented by infinityaction last updated on 24/Apr/22

$${thank}\:{you}\:{sir} \\ $$
