Question Number 161770 by cortano last updated on 22/Dec/21

$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }+\mathrm{2}{x}\right)^{\mathrm{2021}} −\left(\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }−\mathrm{2}{x}\right)^{\mathrm{2021}} }{{x}} \\ $$
Answered by Ar Brandon last updated on 22/Dec/21

$$ \\ $$$${a}^{{n}} −{b}^{{n}} =\left({a}−{b}\right)\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{a}^{{n}−\mathrm{1}−{k}} {b}^{{k}} \\ $$$$\mathscr{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }+\mathrm{2}{x}\right)^{\mathrm{2021}} −\left(\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }−\mathrm{2}{x}\right)^{\mathrm{2021}} }{{x}} \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{4}{x}\underset{{k}=\mathrm{0}} {\overset{\mathrm{2020}} {\sum}}\left(\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }+\mathrm{2}{x}\right)^{\mathrm{2020}−{k}} \left(\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }−\mathrm{2}{x}\right)^{{k}} }{{x}} \\ $$$$\:\:\:\:\:=\mathrm{4}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\underset{{k}=\mathrm{0}} {\overset{\mathrm{2020}} {\sum}}\left(\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }+\mathrm{2}{x}\right)^{\mathrm{2020}−{k}} \left(\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }−\mathrm{2}{x}\right)^{{k}} \\ $$$$\:\:\:\:\:\:=\mathrm{4}\underset{{k}=\mathrm{0}} {\overset{\mathrm{2020}} {\sum}}\left(\mathrm{1}\right)=\mathrm{4}\left(\mathrm{2021}\right)=\mathrm{8084} \\ $$
Answered by qaz last updated on 22/Dec/21
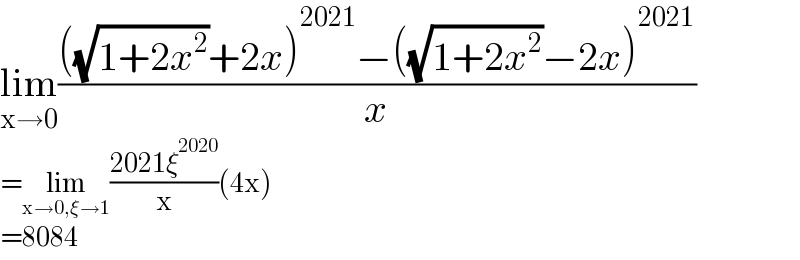
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }+\mathrm{2}{x}\right)^{\mathrm{2021}} −\left(\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }−\mathrm{2}{x}\right)^{\mathrm{2021}} }{{x}} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0},\xi\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{2021}\xi^{\mathrm{2020}} }{\mathrm{x}}\left(\mathrm{4x}\right) \\ $$$$=\mathrm{8084} \\ $$
