Menu Close

lim-x-0-1-3x-1-3-1-2x-x-2-

Tinku Tara 0 Comments
Pin




Question Number 123398 by bemath last updated on 25/Nov/20
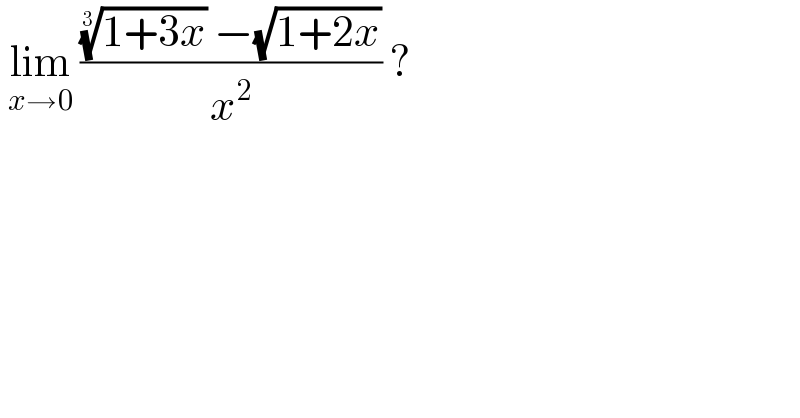
lim_(x→0) ((((1+3x))^(1/3) −(√(1+2x)))/x^2 ) ?
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{3}{x}}\:−\sqrt{\mathrm{1}+\mathrm{2}{x}}}{{x}^{\mathrm{2}} }\:? \\ $$
Answered by Dwaipayan Shikari last updated on 25/Nov/20
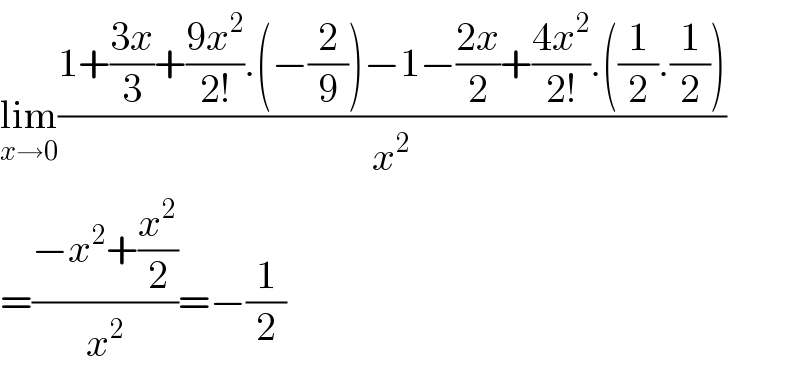
lim_(x→0) ((1+((3x)/3)+((9x^2 )/(2!)).(−(2/9))−1−((2x)/2)+((4x^2 )/(2!)).((1/2).(1/2)))/x^2 ) =((−x^2 +(x^2 /2))/x^2 )=−(1/2)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}+\frac{\mathrm{3}{x}}{\mathrm{3}}+\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}!}.\left(−\frac{\mathrm{2}}{\mathrm{9}}\right)−\mathrm{1}−\frac{\mathrm{2}{x}}{\mathrm{2}}+\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{2}!}.\left(\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}}\right)}{{x}^{\mathrm{2}} } \\ $$$$=\frac{−{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}{{x}^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by TANMAY PANACEA last updated on 25/Nov/20
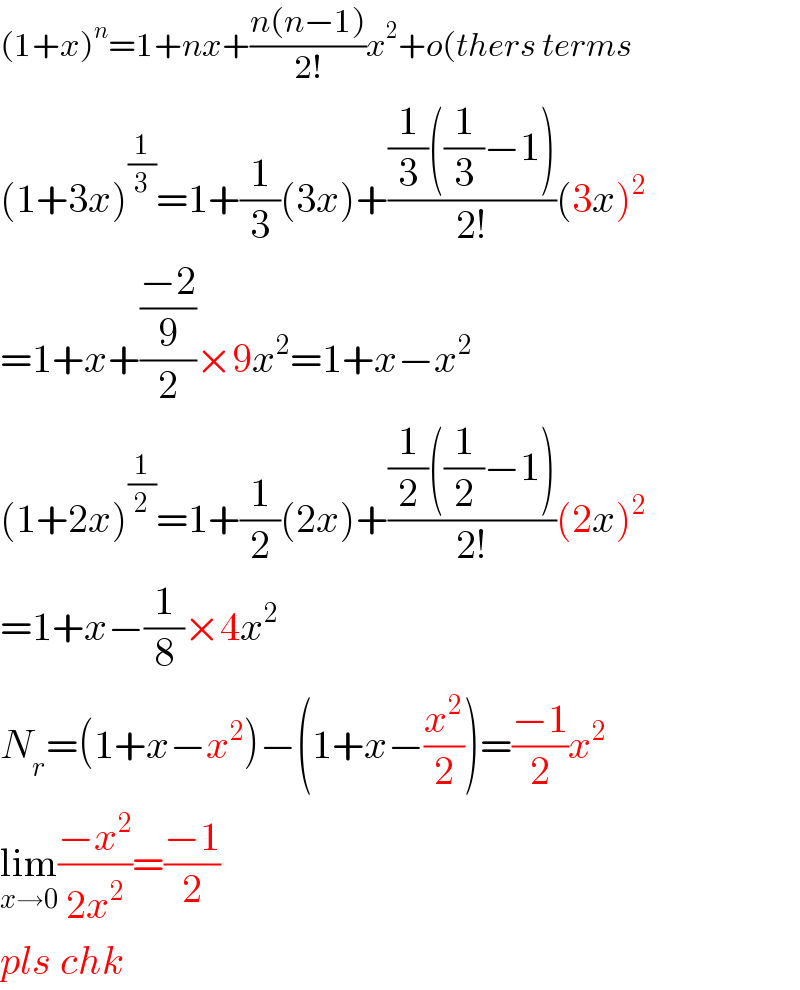
(1+x)^n =1+nx+((n(n−1))/(2!))x^2 +o(thers terms (1+3x)^(1/3) =1+(1/3)(3x)+(((1/3)((1/3)−1))/(2!))(3x)^2 =1+x+(((−2)/9)/2)×9x^2 =1+x−x^2 (1+2x)^(1/2) =1+(1/2)(2x)+(((1/2)((1/2)−1))/(2!))(2x)^2 =1+x−(1/8)×4x^2 N_r =(1+x−x^2 )−(1+x−(x^2 /2))=((−1)/2)x^2 lim_(x→0) ((−x^2 )/(2x^2 ))=((−1)/2) pls chk
$$\left(\mathrm{1}+{x}\right)^{{n}} =\mathrm{1}+{nx}+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} +{o}\left({thers}\:{terms}\right. \\ $$$$\left(\mathrm{1}+\mathrm{3}{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{3}{x}\right)+\frac{\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}\right)}{\mathrm{2}!}\left(\mathrm{3}{x}\right)^{\mathrm{2}} \\ $$$$=\mathrm{1}+{x}+\frac{\frac{−\mathrm{2}}{\mathrm{9}}}{\mathrm{2}}×\mathrm{9}{x}^{\mathrm{2}} =\mathrm{1}+{x}−{x}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+\mathrm{2}{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{x}\right)+\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2}!}\left(\mathrm{2}{x}\right)^{\mathrm{2}} \\ $$$$=\mathrm{1}+{x}−\frac{\mathrm{1}}{\mathrm{8}}×\mathrm{4}{x}^{\mathrm{2}} \\ $$$${N}_{{r}} =\left(\mathrm{1}+{x}−{x}^{\mathrm{2}} \right)−\left(\mathrm{1}+{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)=\frac{−\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−{x}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} }=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$$${pls}\:{chk} \\ $$
Answered by TANMAY PANACEA last updated on 25/Nov/20
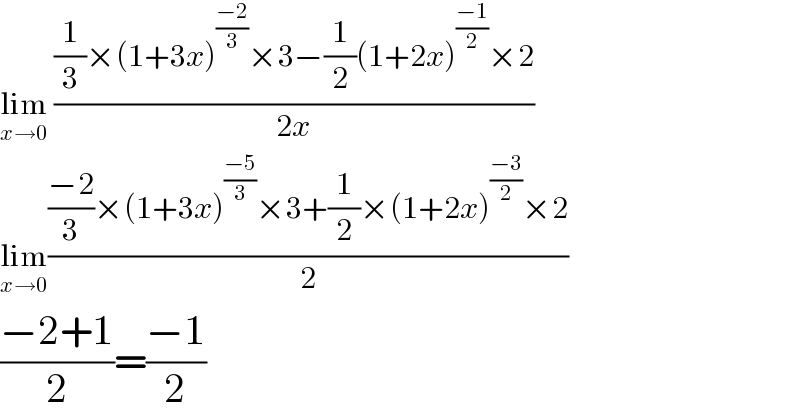
lim_(x→0) (((1/3)×(1+3x)^((−2)/3) ×3−(1/2)(1+2x)^((−1)/2) ×2)/(2x)) lim_(x→0) ((((−2)/3)×(1+3x)^((−5)/3) ×3+(1/2)×(1+2x)^((−3)/2) ×2)/2) ((−2+1)/2)=((−1)/2)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{3}}×\left(\mathrm{1}+\mathrm{3}{x}\right)^{\frac{−\mathrm{2}}{\mathrm{3}}} ×\mathrm{3}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{2}{x}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}} ×\mathrm{2}}{\mathrm{2}{x}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{−\mathrm{2}}{\mathrm{3}}×\left(\mathrm{1}+\mathrm{3}{x}\right)^{\frac{−\mathrm{5}}{\mathrm{3}}} ×\mathrm{3}+\frac{\mathrm{1}}{\mathrm{2}}×\left(\mathrm{1}+\mathrm{2}{x}\right)^{\frac{−\mathrm{3}}{\mathrm{2}}} ×\mathrm{2}}{\mathrm{2}} \\ $$$$\frac{−\mathrm{2}+\mathrm{1}}{\mathrm{2}}=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$
Answered by liberty last updated on 25/Nov/20
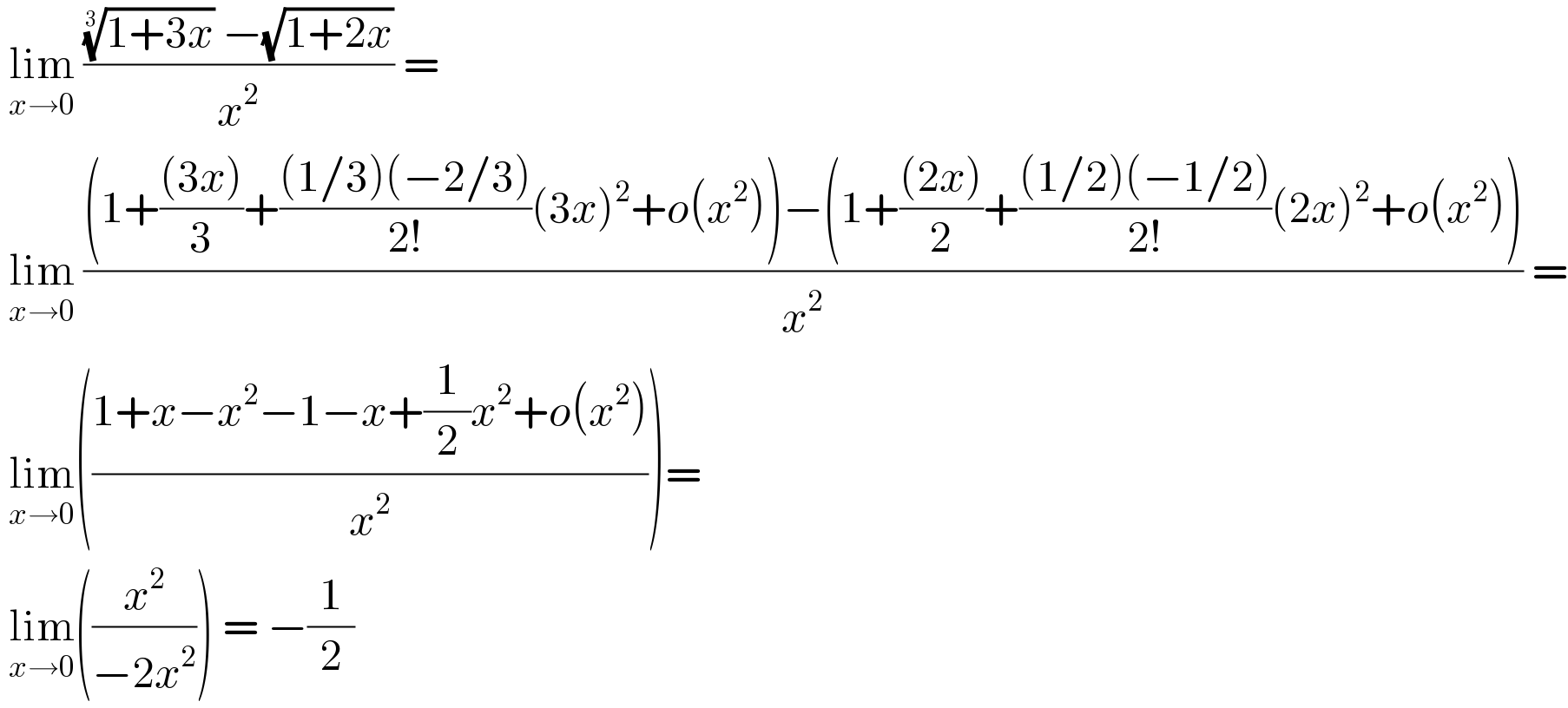
lim_(x→0) ((((1+3x))^(1/3) −(√(1+2x)))/x^2 ) = lim_(x→0) (((1+(((3x))/3)+(((1/3)(−2/3))/(2!))(3x)^2 +o(x^2 ))−(1+(((2x))/2)+(((1/2)(−1/2))/(2!))(2x)^2 +o(x^2 )))/x^2 ) = lim_(x→0) (((1+x−x^2 −1−x+(1/2)x^2 +o(x^2 ))/x^2 ))= lim_(x→0) ((x^2 /(−2x^2 ))) = −(1/2)
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{3}{x}}\:−\sqrt{\mathrm{1}+\mathrm{2}{x}}}{{x}^{\mathrm{2}} }\:=\: \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\frac{\left(\mathrm{3}{x}\right)}{\mathrm{3}}+\frac{\left(\mathrm{1}/\mathrm{3}\right)\left(−\mathrm{2}/\mathrm{3}\right)}{\mathrm{2}!}\left(\mathrm{3}{x}\right)^{\mathrm{2}} +{o}\left({x}^{\mathrm{2}} \right)\right)−\left(\mathrm{1}+\frac{\left(\mathrm{2}{x}\right)}{\mathrm{2}}+\frac{\left(\mathrm{1}/\mathrm{2}\right)\left(−\mathrm{1}/\mathrm{2}\right)}{\mathrm{2}!}\left(\mathrm{2}{x}\right)^{\mathrm{2}} +{o}\left({x}^{\mathrm{2}} \right)\right)}{{x}^{\mathrm{2}} }\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}+{x}−{x}^{\mathrm{2}} −\mathrm{1}−{x}+\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +{o}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }\right)= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{x}^{\mathrm{2}} }{−\mathrm{2}{x}^{\mathrm{2}} }\right)\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by Bird last updated on 25/Nov/20
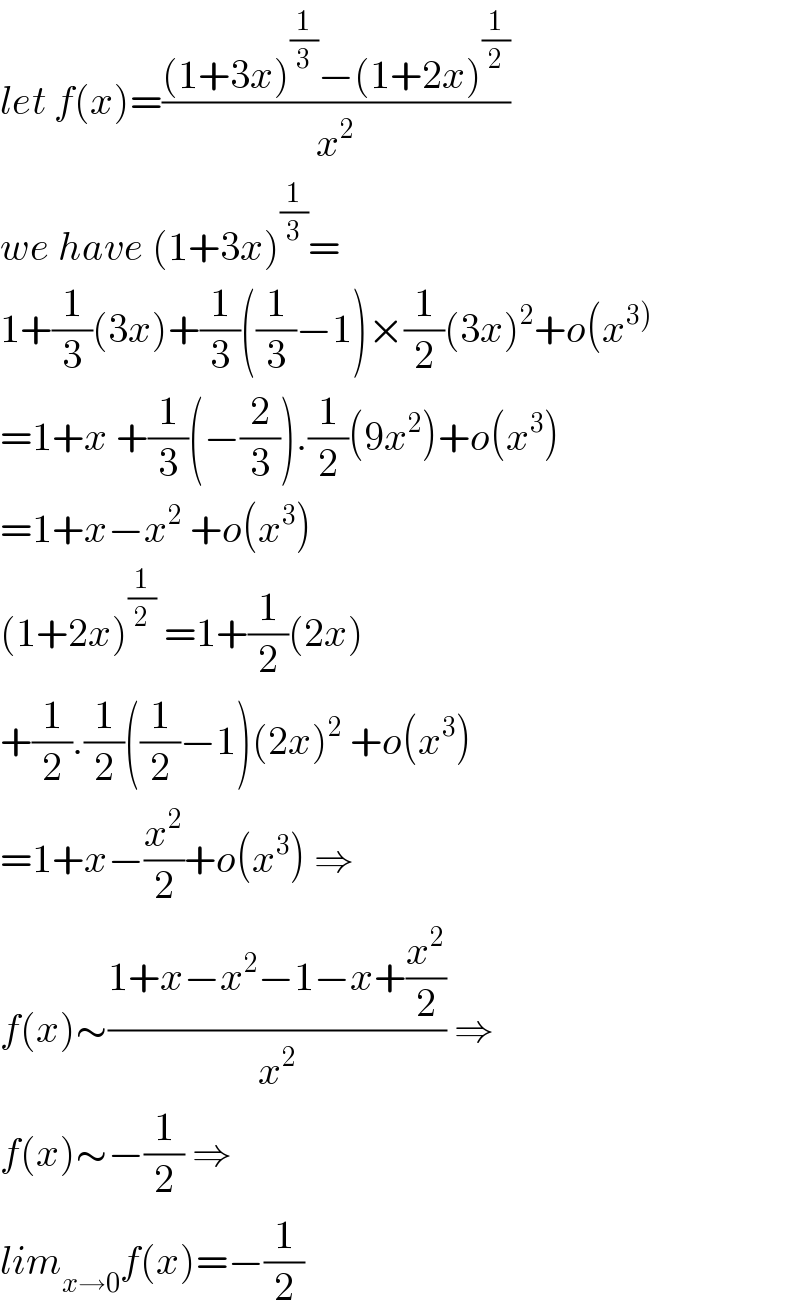
let f(x)=(((1+3x)^(1/3) −(1+2x)^(1/2) )/x^2 ) we have (1+3x)^(1/3) = 1+(1/3)(3x)+(1/3)((1/3)−1)×(1/2)(3x)^2 +o(x^(3)) =1+x +(1/3)(−(2/3)).(1/2)(9x^2 )+o(x^3 ) =1+x−x^2 +o(x^3 ) (1+2x)^(1/2) =1+(1/2)(2x) +(1/2).(1/2)((1/2)−1)(2x)^2 +o(x^3 ) =1+x−(x^2 /2)+o(x^3 ) ⇒ f(x)∼((1+x−x^2 −1−x+(x^2 /2))/x^2 ) ⇒ f(x)∼−(1/2) ⇒ lim_(x→0) f(x)=−(1/2)
$${let}\:{f}\left({x}\right)=\frac{\left(\mathrm{1}+\mathrm{3}{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\left(\mathrm{1}+\mathrm{2}{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{{x}^{\mathrm{2}} } \\ $$$${we}\:{have}\:\left(\mathrm{1}+\mathrm{3}{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} = \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{3}{x}\right)+\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}\right)×\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}{x}\right)^{\mathrm{2}} +{o}\left({x}^{\left.\mathrm{3}\right)} \right. \\ $$$$=\mathrm{1}+{x}\:+\frac{\mathrm{1}}{\mathrm{3}}\left(−\frac{\mathrm{2}}{\mathrm{3}}\right).\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{9}{x}^{\mathrm{2}} \right)+{o}\left({x}^{\mathrm{3}} \right) \\ $$$$=\mathrm{1}+{x}−{x}^{\mathrm{2}} \:+{o}\left({x}^{\mathrm{3}} \right) \\ $$$$\left(\mathrm{1}+\mathrm{2}{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{x}\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)\left(\mathrm{2}{x}\right)^{\mathrm{2}} \:+{o}\left({x}^{\mathrm{3}} \right) \\ $$$$=\mathrm{1}+{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{o}\left({x}^{\mathrm{3}} \right)\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\frac{\mathrm{1}+{x}−{x}^{\mathrm{2}} −\mathrm{1}−{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}{{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$${f}\left({x}\right)\sim−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *