Question Number 144816 by liberty last updated on 29/Jun/21
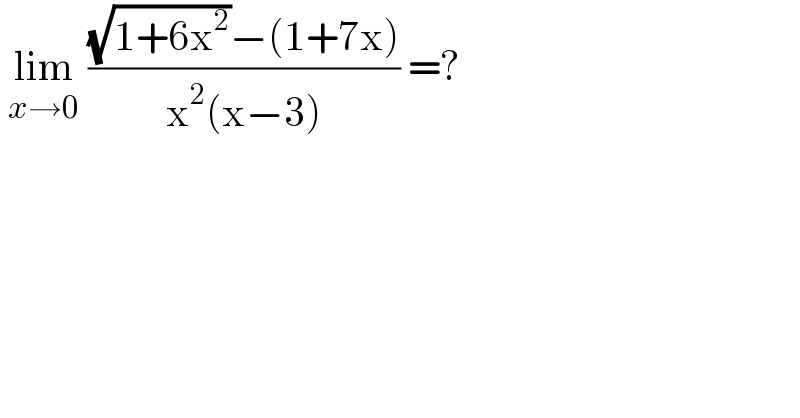
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}+\mathrm{6x}^{\mathrm{2}} }−\left(\mathrm{1}+\mathrm{7x}\right)}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\mathrm{3}\right)}\:=? \\ $$
Answered by imjagoll last updated on 29/Jun/21
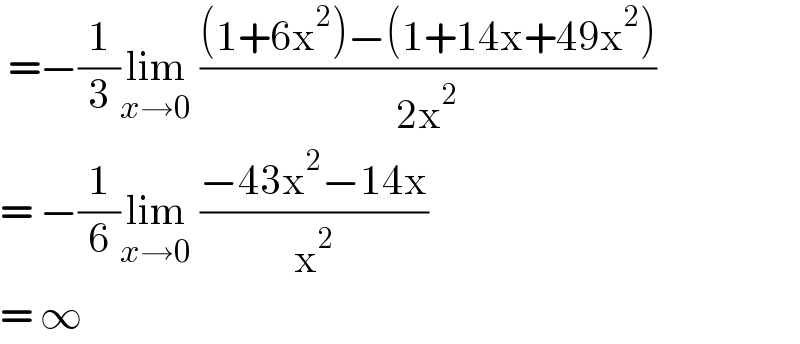
$$\:=−\frac{\mathrm{1}}{\mathrm{3}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\mathrm{6x}^{\mathrm{2}} \right)−\left(\mathrm{1}+\mathrm{14x}+\mathrm{49x}^{\mathrm{2}} \right)}{\mathrm{2x}^{\mathrm{2}} } \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{6}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{43x}^{\mathrm{2}} −\mathrm{14x}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\:\infty\: \\ $$
Answered by mathmax by abdo last updated on 29/Jun/21
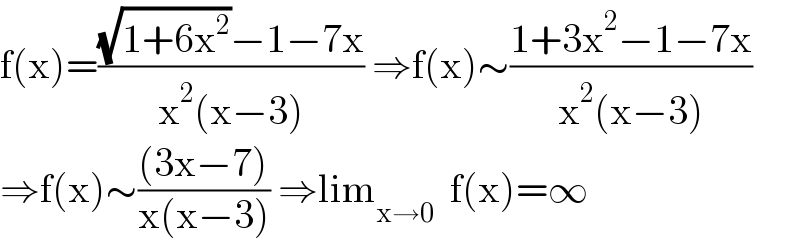
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\sqrt{\mathrm{1}+\mathrm{6x}^{\mathrm{2}} }−\mathrm{1}−\mathrm{7x}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\mathrm{3}\right)}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{1}+\mathrm{3x}^{\mathrm{2}} −\mathrm{1}−\mathrm{7x}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\mathrm{3}\right)} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\left(\mathrm{3x}−\mathrm{7}\right)}{\mathrm{x}\left(\mathrm{x}−\mathrm{3}\right)}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\mathrm{f}\left(\mathrm{x}\right)=\infty \\ $$
