Question Number 115889 by bemath last updated on 29/Sep/20
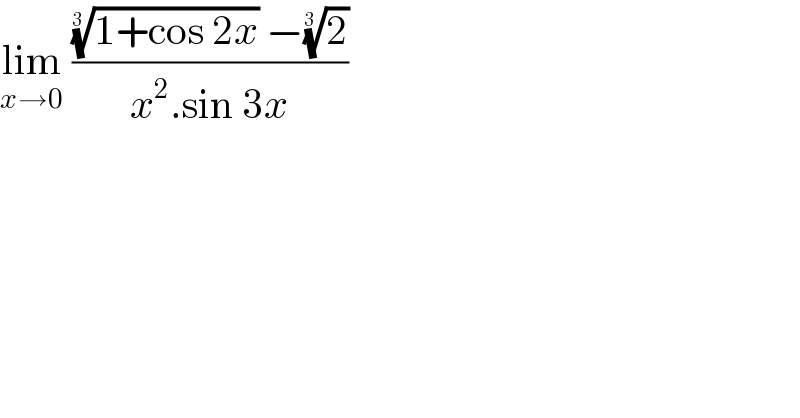
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}}\:−\sqrt[{\mathrm{3}\:}]{\mathrm{2}}}{{x}^{\mathrm{2}} .\mathrm{sin}\:\mathrm{3}{x}} \\ $$
Answered by bemath last updated on 29/Sep/20
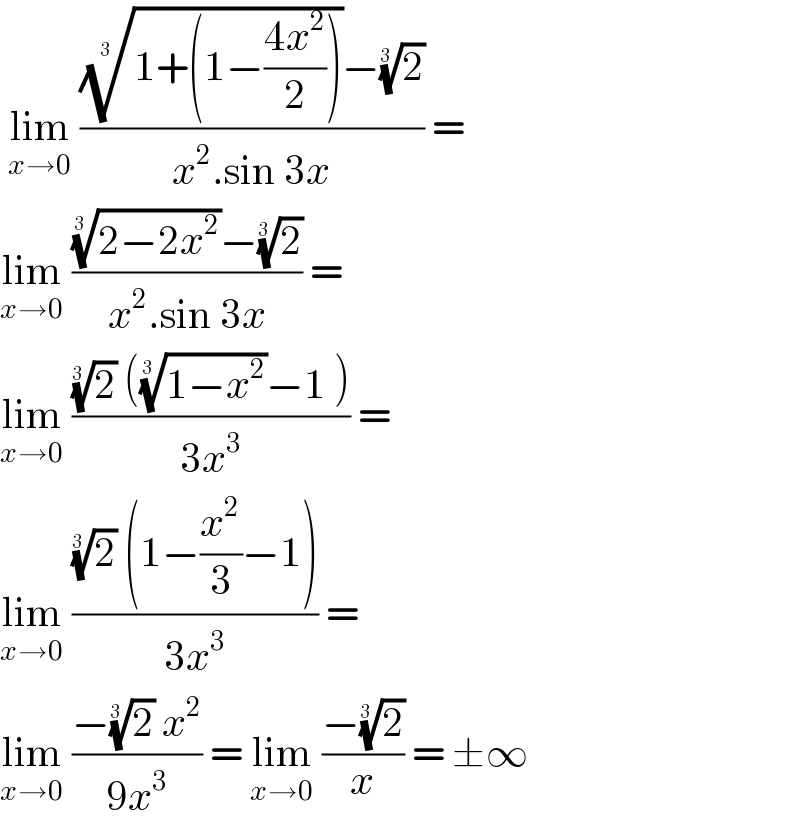
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{1}+\left(\mathrm{1}−\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{2}}\right)}−\sqrt[{\mathrm{3}\:}]{\mathrm{2}}}{{x}^{\mathrm{2}} .\mathrm{sin}\:\mathrm{3}{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{2}−\mathrm{2}{x}^{\mathrm{2}} }−\sqrt[{\mathrm{3}\:}]{\mathrm{2}}}{{x}^{\mathrm{2}} .\mathrm{sin}\:\mathrm{3}{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{2}}\:\left(\sqrt[{\mathrm{3}\:}]{\mathrm{1}−{x}^{\mathrm{2}} }−\mathrm{1}\:\right)}{\mathrm{3}{x}^{\mathrm{3}} }\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{2}}\:\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−\mathrm{1}\right)}{\mathrm{3}{x}^{\mathrm{3}} }\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\sqrt[{\mathrm{3}\:}]{\mathrm{2}}\:{x}^{\mathrm{2}} }{\mathrm{9}{x}^{\mathrm{3}} }\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\sqrt[{\mathrm{3}\:}]{\mathrm{2}}}{{x}}\:=\:\pm\infty \\ $$
