Question Number 92239 by jagoll last updated on 05/May/20
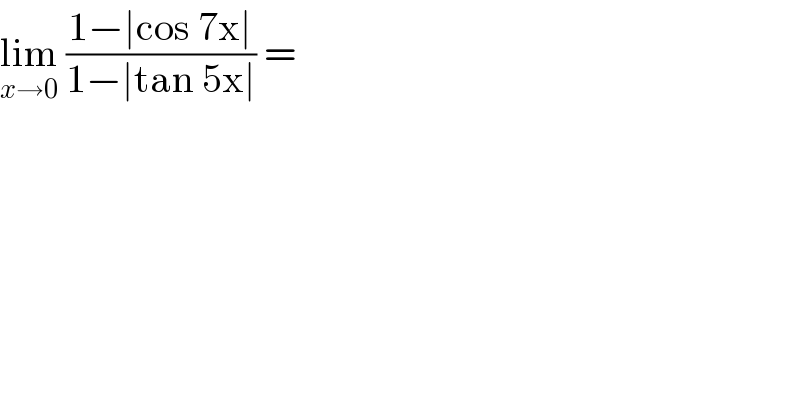
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mid\mathrm{cos}\:\mathrm{7x}\mid}{\mathrm{1}−\mid\mathrm{tan}\:\mathrm{5x}\mid}\:=\: \\ $$
Commented by john santu last updated on 05/May/20
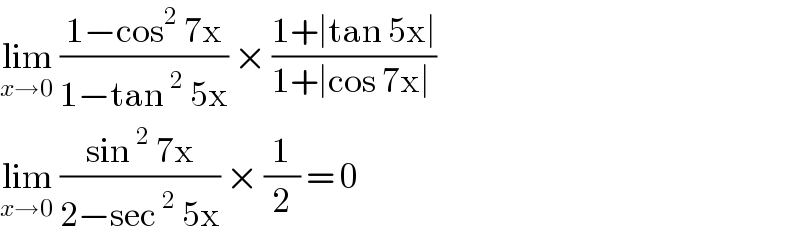
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\mathrm{7x}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \:\mathrm{5x}}\:×\:\frac{\mathrm{1}+\mid\mathrm{tan}\:\mathrm{5x}\mid}{\mathrm{1}+\mid\mathrm{cos}\:\mathrm{7x}\mid\:} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:^{\mathrm{2}} \:\mathrm{7x}}{\mathrm{2}−\mathrm{sec}\:^{\mathrm{2}} \:\mathrm{5x}}\:×\:\frac{\mathrm{1}}{\mathrm{2}}\:=\:\mathrm{0} \\ $$
Commented by john santu last updated on 05/May/20
������
Commented by Prithwish Sen 1 last updated on 05/May/20
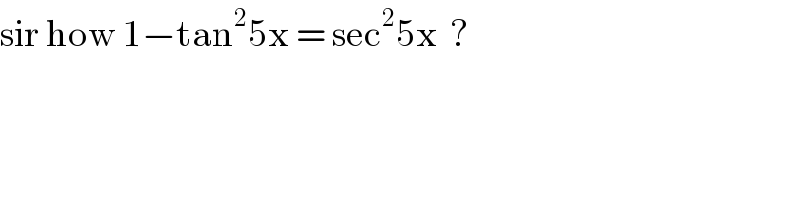
$$\mathrm{sir}\:\mathrm{how}\:\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{5x}\:=\:\mathrm{sec}^{\mathrm{2}} \mathrm{5x}\:\:? \\ $$
Commented by john santu last updated on 05/May/20

$$\mathrm{haha}..\mathrm{typo} \\ $$
Commented by Prithwish Sen 1 last updated on 05/May/20
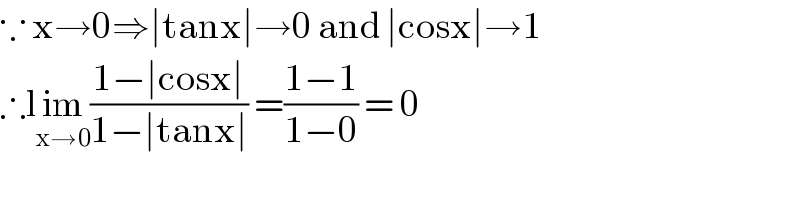
$$\because\:\mathrm{x}\rightarrow\mathrm{0}\Rightarrow\mid\mathrm{tanx}\mid\rightarrow\mathrm{0}\:\mathrm{and}\:\mid\mathrm{cosx}\mid\rightarrow\mathrm{1} \\ $$$$\therefore\mathrm{l}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{im}}\frac{\mathrm{1}−\mid\mathrm{cosx}\mid}{\mathrm{1}−\mid\mathrm{tanx}\mid}\:=\frac{\mathrm{1}−\mathrm{1}}{\mathrm{1}−\mathrm{0}}\:=\:\mathrm{0} \\ $$
