Question Number 115999 by bemath last updated on 30/Sep/20
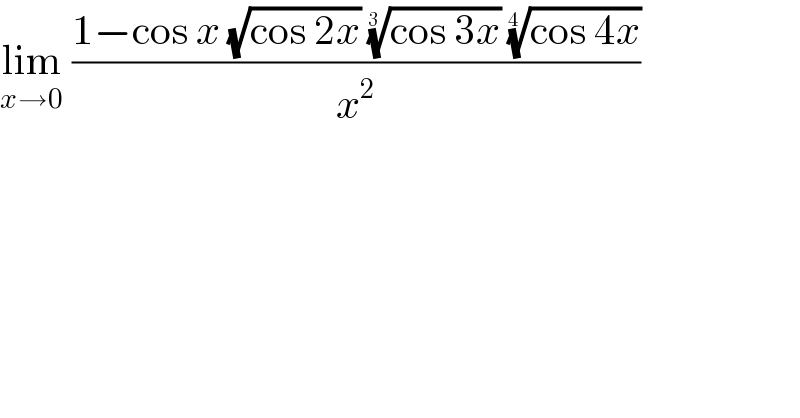
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:{x}\:\sqrt{\mathrm{cos}\:\mathrm{2}{x}}\:\sqrt[{\mathrm{3}\:}]{\mathrm{cos}\:\mathrm{3}{x}}\:\sqrt[{\mathrm{4}\:}]{\mathrm{cos}\:\mathrm{4}{x}}}{{x}^{\mathrm{2}} } \\ $$
Answered by bobhans last updated on 30/Sep/20
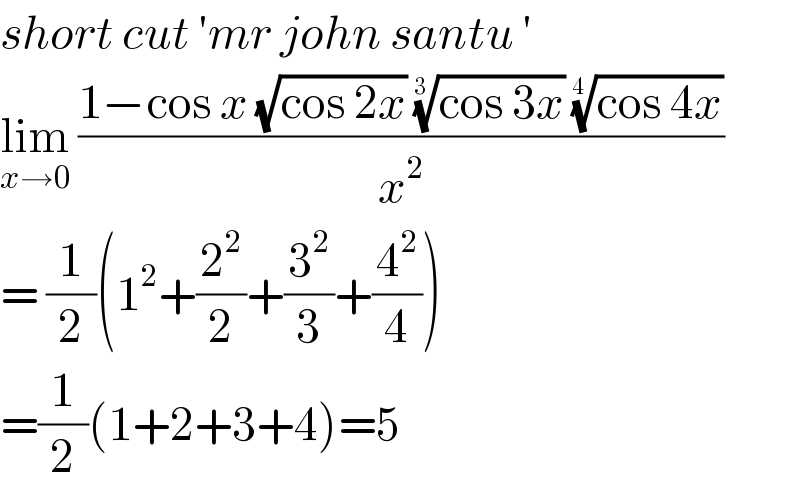
$${short}\:{cut}\:'{mr}\:{john}\:{santu}\:' \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:{x}\:\sqrt{\mathrm{cos}\:\mathrm{2}{x}}\:\sqrt[{\mathrm{3}\:}]{\mathrm{cos}\:\mathrm{3}{x}}\:\sqrt[{\mathrm{4}\:}]{\mathrm{cos}\:\mathrm{4}{x}}}{{x}^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}^{\mathrm{2}} +\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{3}}+\frac{\mathrm{4}^{\mathrm{2}} }{\mathrm{4}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}\right)=\mathrm{5} \\ $$
