lim-x-0-1-cos-x-cos-2x-cos-3x-cos-px-x-2-

Question Number 146376 by iloveisrael last updated on 13/Jul/21

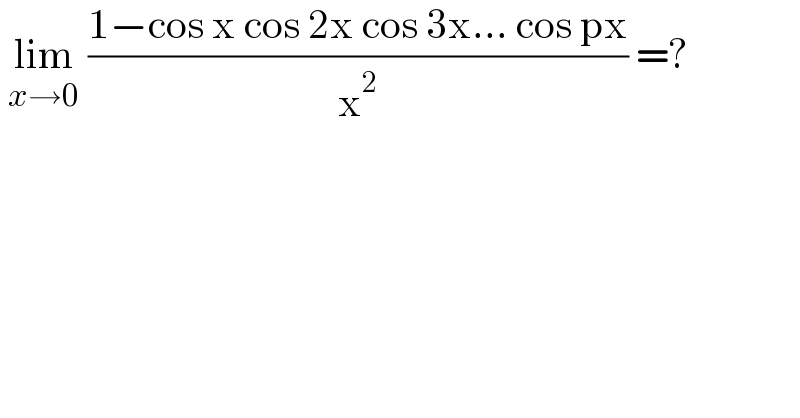
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{2x}\:\mathrm{cos}\:\mathrm{3x}…\:\mathrm{cos}\:\mathrm{px}}{\mathrm{x}^{\mathrm{2}} }\:=? \\ $$

Answered by gsk2684 last updated on 13/Jul/21

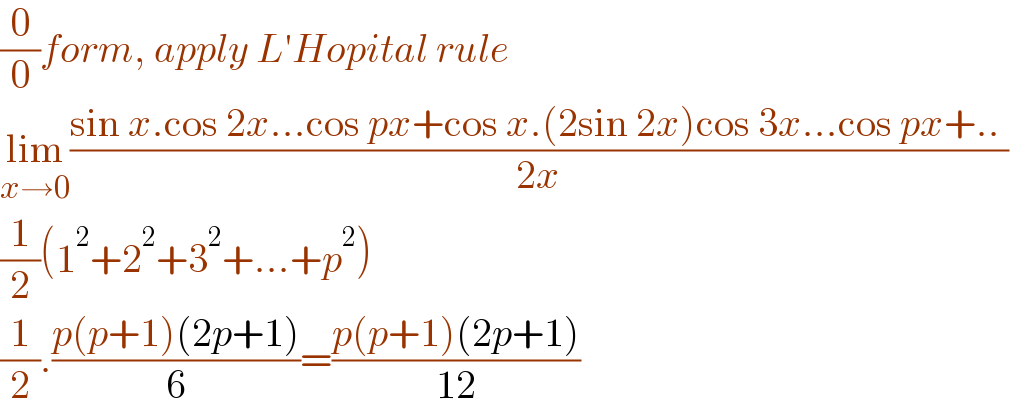
(0/0)form, apply L′Hopital rule lim_(x→0) ((sin x.cos 2x...cos px+cos x.(2sin 2x)cos 3x...cos px+.. )/(2x)) (1/2)(1^2 +2^2 +3^2 +...+p^2 ) (1/2).((p(p+1)(2p+1))/6)=((p(p+1)(2p+1))/(12))

$$\frac{\mathrm{0}}{\mathrm{0}}{form},\:{apply}\:{L}'{Hopital}\:{rule} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{x}.\mathrm{cos}\:\mathrm{2}{x}…\mathrm{cos}\:{px}+\mathrm{cos}\:{x}.\left(\mathrm{2sin}\:\mathrm{2}{x}\right)\mathrm{cos}\:\mathrm{3}{x}…\mathrm{cos}\:{px}+..\:}{\mathrm{2}{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +…+{p}^{\mathrm{2}} \right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}.\frac{{p}\left({p}+\mathrm{1}\right)\left(\mathrm{2}{p}+\mathrm{1}\right)}{\mathrm{6}}=\frac{{p}\left({p}+\mathrm{1}\right)\left(\mathrm{2}{p}+\mathrm{1}\right)}{\mathrm{12}} \\ $$

Commented by iloveisrael last updated on 13/Jul/21