Menu Close

lim-x-0-1-cos-x-cos-2x-x-sin-x-

Tinku Tara 0 Comments
Pin




Question Number 126685 by bramlexs22 last updated on 23/Dec/20
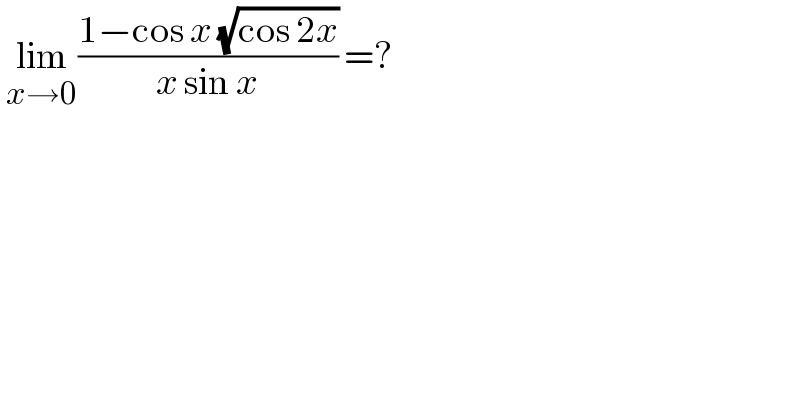
lim_(x→0) ((1−cos x (√(cos 2x)))/(x sin x)) =?
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:{x}\:\sqrt{\mathrm{cos}\:\mathrm{2}{x}}}{{x}\:\mathrm{sin}\:{x}}\:=? \\ $$
Answered by liberty last updated on 23/Dec/20
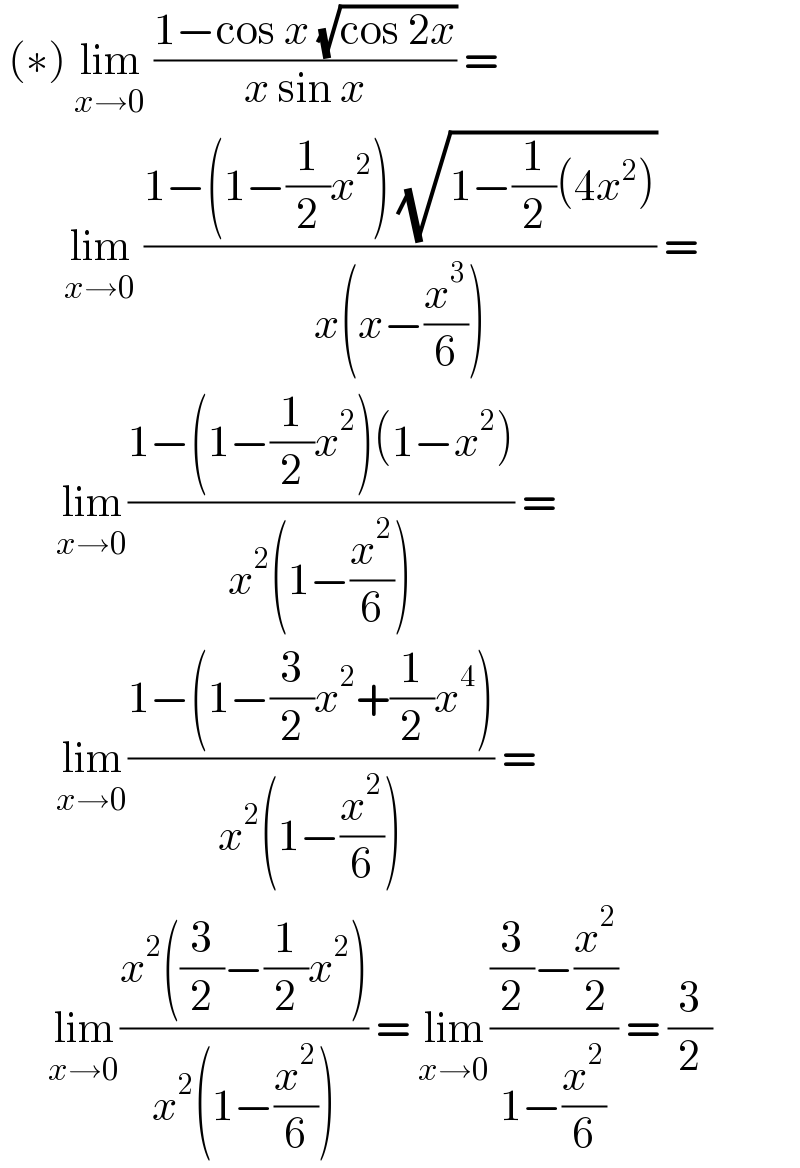
(∗) lim_(x→0) ((1−cos x (√(cos 2x)))/(x sin x)) = lim_(x→0) ((1−(1−(1/2)x^2 ) (√(1−(1/2)(4x^2 ))))/(x(x−(x^3 /6)))) = lim_(x→0) ((1−(1−(1/2)x^2 )(1−x^2 ))/(x^2 (1−(x^2 /6)))) = lim_(x→0) ((1−(1−(3/2)x^2 +(1/2)x^4 ))/(x^2 (1−(x^2 /6)))) = lim_(x→0) ((x^2 ((3/2)−(1/2)x^2 ))/(x^2 (1−(x^2 /6)))) = lim_(x→0) (((3/2)−(x^2 /2))/(1−(x^2 /6))) = (3/2)
$$\:\left(\ast\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:{x}\:\sqrt{\mathrm{cos}\:\mathrm{2}{x}}}{{x}\:\mathrm{sin}\:{x}}\:= \\ $$$$\:\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right)\:\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{4}{x}^{\mathrm{2}} \right)}}{{x}\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)}\:= \\ $$$$\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\right)}\:= \\ $$$$\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{4}} \right)}{{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\right)}\:= \\ $$$$\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\right)}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{3}}{\mathrm{2}}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}}\:=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Answered by Dwaipayan Shikari last updated on 23/Dec/20
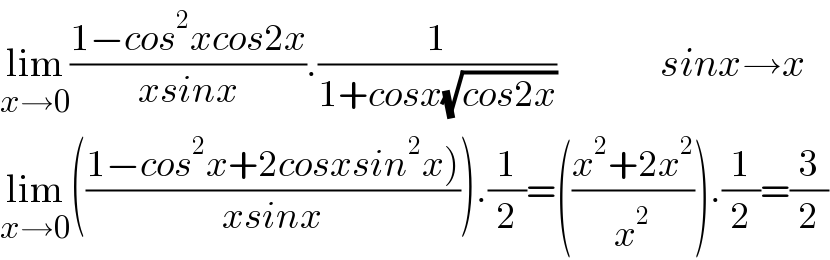
lim_(x→0) ((1−cos^2 xcos2x)/(xsinx)).(1/(1+cosx(√(cos2x)))) sinx→x lim_(x→0) (((1−cos^2 x+2cosxsin^2 x))/(xsinx))).(1/2)=(((x^2 +2x^2 )/x^2 )).(1/2)=(3/2)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−{cos}^{\mathrm{2}} {xcos}\mathrm{2}{x}}{{xsinx}}.\frac{\mathrm{1}}{\mathrm{1}+{cosx}\sqrt{{cos}\mathrm{2}{x}}}\:\:\:\:\:\:\:\:\:\:\:\:\:{sinx}\rightarrow{x} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left.\mathrm{1}−{cos}^{\mathrm{2}} {x}+\mathrm{2}{cosxsin}^{\mathrm{2}} {x}\right)}{{xsinx}}\right).\frac{\mathrm{1}}{\mathrm{2}}=\left(\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right).\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Answered by bramlexs22 last updated on 23/Dec/20
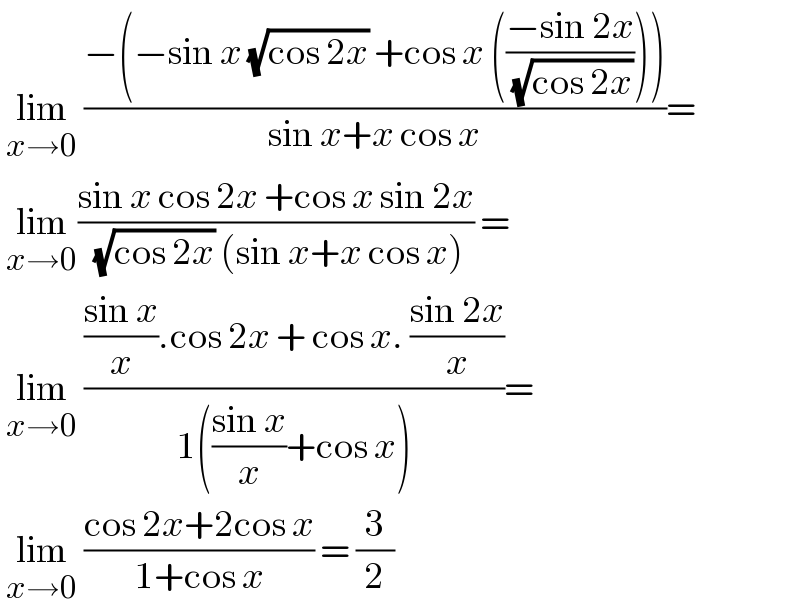
lim_(x→0) ((−(−sin x (√(cos 2x)) +cos x (((−sin 2x)/( (√(cos 2x)))))))/(sin x+x cos x))= lim_(x→0) ((sin x cos 2x +cos x sin 2x)/( (√(cos 2x)) (sin x+x cos x))) = lim_(x→0) ((((sin x)/x).cos 2x + cos x. ((sin 2x)/x))/(1(((sin x)/x)+cos x)))= lim_(x→0) ((cos 2x+2cos x)/(1+cos x)) = (3/2)
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\left(−\mathrm{sin}\:{x}\:\sqrt{\mathrm{cos}\:\mathrm{2}{x}}\:+\mathrm{cos}\:{x}\:\left(\frac{−\mathrm{sin}\:\mathrm{2}{x}}{\:\sqrt{\mathrm{cos}\:\mathrm{2}{x}}}\right)\right)}{\mathrm{sin}\:{x}+{x}\:\mathrm{cos}\:{x}}= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{x}\:\mathrm{cos}\:\mathrm{2}{x}\:+\mathrm{cos}\:{x}\:\mathrm{sin}\:\mathrm{2}{x}}{\:\sqrt{\mathrm{cos}\:\mathrm{2}{x}}\:\left(\mathrm{sin}\:{x}+{x}\:\mathrm{cos}\:{x}\right)}\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{sin}\:{x}}{{x}}.\mathrm{cos}\:\mathrm{2}{x}\:+\:\mathrm{cos}\:{x}.\:\frac{\mathrm{sin}\:\mathrm{2}{x}}{{x}}}{\mathrm{1}\left(\frac{\mathrm{sin}\:{x}}{{x}}+\mathrm{cos}\:{x}\right)}= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\mathrm{2}{x}+\mathrm{2cos}\:{x}}{\mathrm{1}+\mathrm{cos}\:{x}}\:=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 24/Dec/20
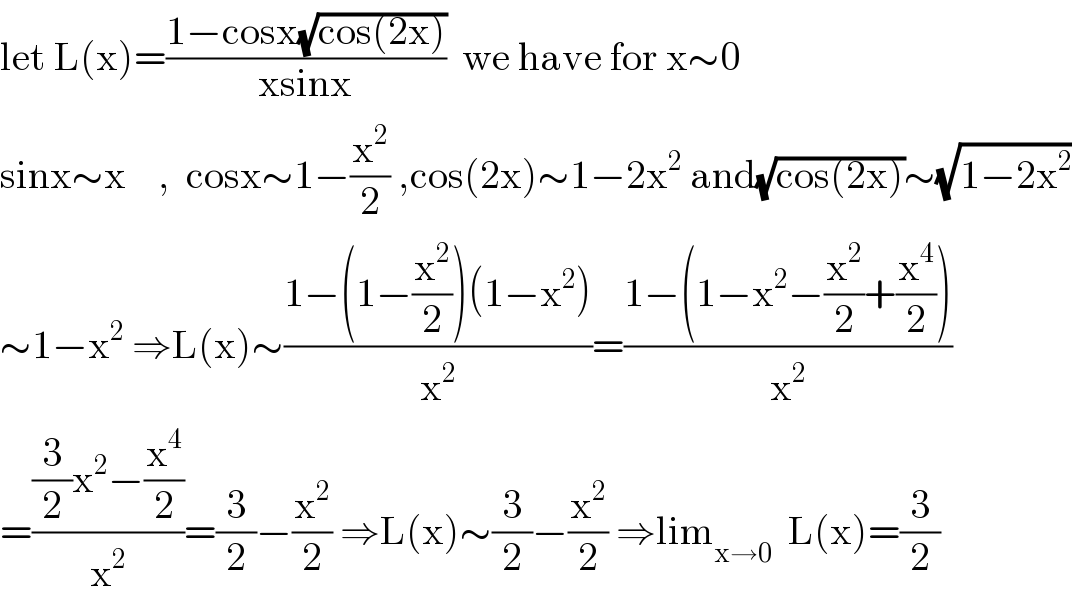
let L(x)=((1−cosx(√(cos(2x))))/(xsinx)) we have for x∼0 sinx∼x , cosx∼1−(x^2 /2) ,cos(2x)∼1−2x^2 and(√(cos(2x)))∼(√(1−2x^2 )) ∼1−x^2 ⇒L(x)∼((1−(1−(x^2 /2))(1−x^2 ))/x^2 )=((1−(1−x^2 −(x^2 /2)+(x^4 /2)))/x^2 ) =(((3/2)x^2 −(x^4 /2))/x^2 )=(3/2)−(x^2 /2) ⇒L(x)∼(3/2)−(x^2 /2) ⇒lim_(x→0) L(x)=(3/2)
$$\mathrm{let}\:\mathrm{L}\left(\mathrm{x}\right)=\frac{\mathrm{1}−\mathrm{cosx}\sqrt{\mathrm{cos}\left(\mathrm{2x}\right)}}{\mathrm{xsinx}}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{for}\:\mathrm{x}\sim\mathrm{0} \\ $$$$\mathrm{sinx}\sim\mathrm{x}\:\:\:\:,\:\:\mathrm{cosx}\sim\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:,\mathrm{cos}\left(\mathrm{2x}\right)\sim\mathrm{1}−\mathrm{2x}^{\mathrm{2}} \:\mathrm{and}\sqrt{\mathrm{cos}\left(\mathrm{2x}\right)}\sim\sqrt{\mathrm{1}−\mathrm{2x}^{\mathrm{2}} } \\ $$$$\sim\mathrm{1}−\mathrm{x}^{\mathrm{2}} \:\Rightarrow\mathrm{L}\left(\mathrm{x}\right)\sim\frac{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} }=\frac{\mathrm{1}−\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{2}}\right)}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{2}}}{\mathrm{x}^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{L}\left(\mathrm{x}\right)\sim\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\mathrm{L}\left(\mathrm{x}\right)=\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *