Question Number 58671 by Mikael_Marshall last updated on 27/Apr/19
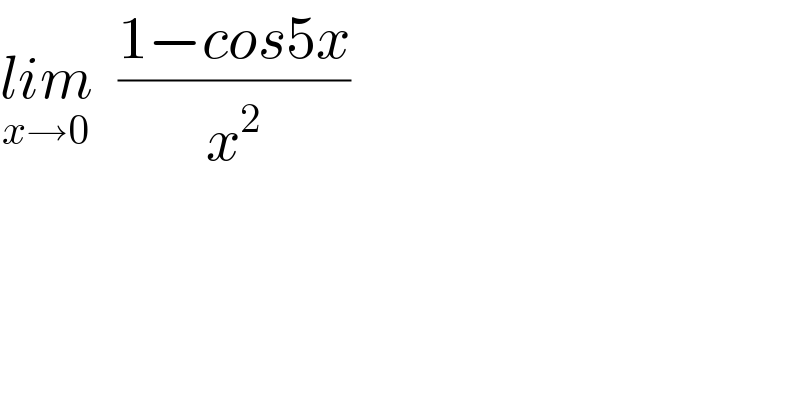
$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\:\frac{\mathrm{1}−{cos}\mathrm{5}{x}}{{x}^{\mathrm{2}} } \\ $$
Commented by maxmathsup by imad last updated on 27/Apr/19

$${we}\:{have}\:\mathrm{1}−{cos}\left(\mathrm{5}{x}\right)\:\sim\:\frac{\left(\mathrm{5}{x}\right)^{\mathrm{2}} }{\mathrm{2}}\:\:\:\left({x}\:\in{V}\left(\mathrm{0}\right)\right)\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\frac{\mathrm{1}−{cos}\left(\mathrm{5}{x}\right)}{{x}^{\mathrm{2}} }\:=\frac{\mathrm{25}}{\mathrm{2}} \\ $$
Commented by Mikael_Marshall last updated on 28/Apr/19

$${thanks}\:{Sir} \\ $$
Answered by mr W last updated on 27/Apr/19

$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{5}\:\mathrm{sin}\:\mathrm{5}{x}}{\mathrm{2}{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{5}{x}}{\mathrm{5}{x}}×\frac{\mathrm{25}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{25}}{\mathrm{2}} \\ $$
Commented by Mikael_Marshall last updated on 27/Apr/19

$${thanks}\:{Sir} \\ $$
Answered by ajfour last updated on 27/Apr/19

$$=\frac{\mathrm{25}}{\mathrm{4}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{5x}}{\mathrm{2}}\right)}{\left(\frac{\mathrm{5x}}{\mathrm{2}}\right)^{\mathrm{2}} }\:=\frac{\mathrm{25}}{\mathrm{4}}×\mathrm{2}=\frac{\mathrm{25}}{\mathrm{2}}\:. \\ $$
Commented by Mikael_Marshall last updated on 27/Apr/19

$${thank}\:{you}\:{Sir} \\ $$
Answered by malwaan last updated on 28/Apr/19
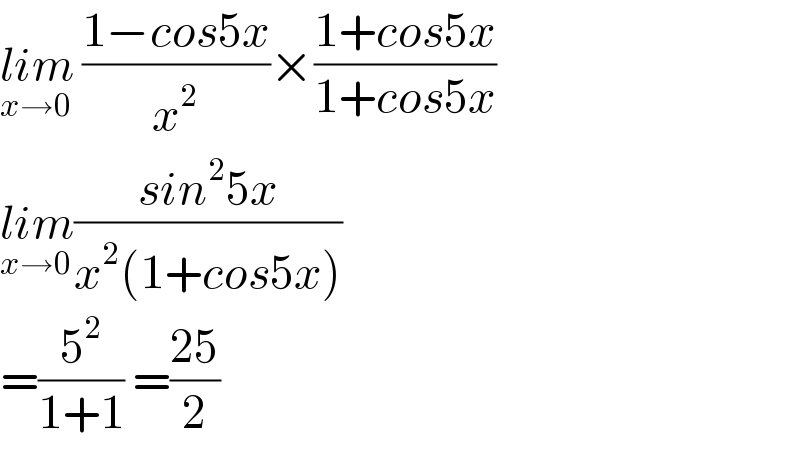
$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{\mathrm{1}−{cos}\mathrm{5}{x}}{{x}^{\mathrm{2}} }×\frac{\mathrm{1}+{cos}\mathrm{5}{x}}{\mathrm{1}+{cos}\mathrm{5}{x}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{sin}^{\mathrm{2}} \mathrm{5}{x}}{{x}^{\mathrm{2}} \left(\mathrm{1}+{cos}\mathrm{5}{x}\right)} \\ $$$$=\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{1}+\mathrm{1}}\:=\frac{\mathrm{25}}{\mathrm{2}} \\ $$
Commented by Mikael_Marshall last updated on 28/Apr/19

$${thankz}\:{Sir} \\ $$
