Question Number 168464 by Altaf180 last updated on 11/Apr/22
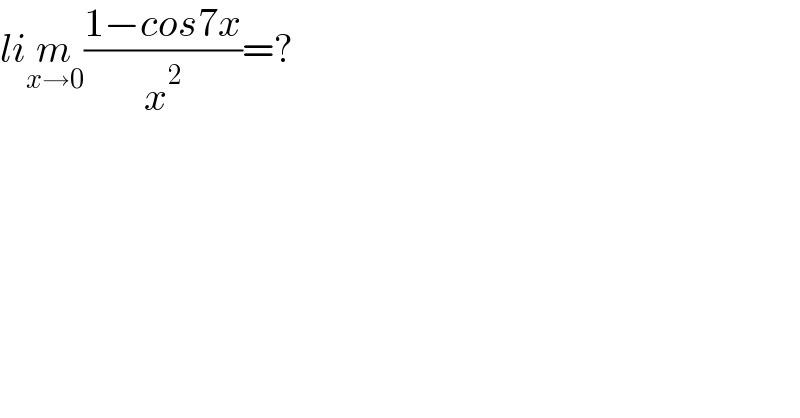
$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{\mathrm{1}−{cos}\mathrm{7}{x}}{{x}^{\mathrm{2}} }=? \\ $$
Commented by safojontoshtemirov last updated on 11/Apr/22

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}2}\left({sin}^{\mathrm{2}} \frac{\mathrm{7}{x}}{\mathrm{2}}\right)/{x}^{\mathrm{2}} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}2}\centerdot\frac{\mathrm{49}}{\mathrm{4}}\left(\frac{{sin}\frac{\mathrm{7}{x}}{\mathrm{2}}}{\frac{\mathrm{7}{x}}{\mathrm{2}}}\right)^{\mathrm{2}} = \\ $$$$=\frac{\mathrm{49}}{\mathrm{2}}\:\: \\ $$
Answered by malwan last updated on 14/Apr/22
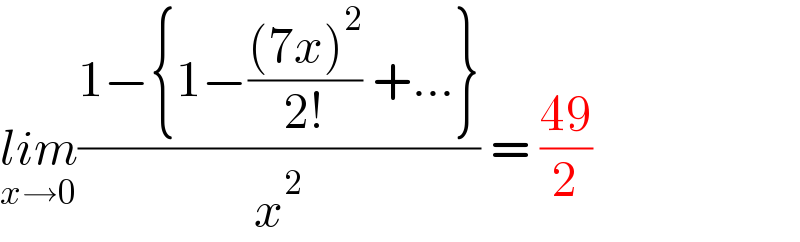
$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{1}−\left\{\mathrm{1}−\frac{\left(\mathrm{7}{x}\right)^{\mathrm{2}} }{\mathrm{2}!}\:+…\right\}}{{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{49}}{\mathrm{2}} \\ $$
