Question Number 80455 by jagoll last updated on 03/Feb/20
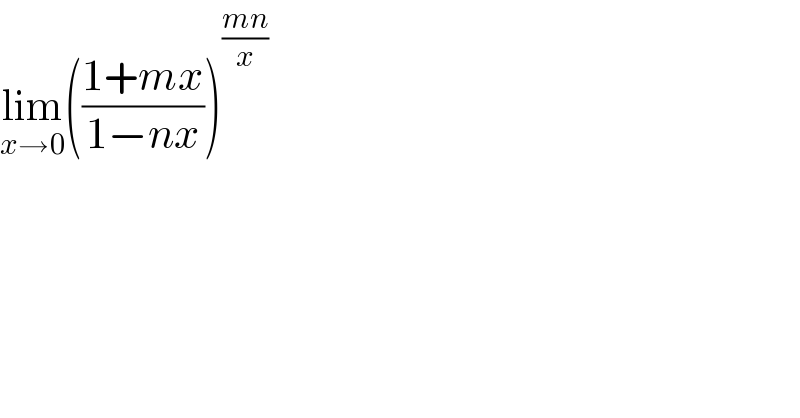
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}+{mx}}{\mathrm{1}−{nx}}\right)^{\frac{{mn}}{{x}}} \\ $$
Commented by mr W last updated on 03/Feb/20
![lim_(x→0) (((1+mx)/(1−nx)))^((mn)/x) =lim_(x→0) ((((1/x)+m)/((1/x)−n)))^((mn)/x) =lim_(t→∞) [(((t+m)/(t−n)))^t ]^(mn) =lim_(t→∞) [(1+((m+n)/(t−n)))^t ]^(mn) =lim_(t→∞) [(1+((m+n)/(t−n)))^(t−n) (1+((m+n)/(t−n)))^n ]^(mn) =lim_(t→∞) [(1+(1/((t−n)/(m+n))))^((t−n)/(m+n)) (1+((m+n)/(t−n)))^(n/(m+n)) ]^(mn(m+n)) =[e(1+0)^(n/(m+n)) ]^(mn(m+n)) =e^(mn(m+n))](https://www.tinkutara.com/question/Q80460.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}+{mx}}{\mathrm{1}−{nx}}\right)^{\frac{{mn}}{{x}}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\frac{\mathrm{1}}{{x}}+{m}}{\frac{\mathrm{1}}{{x}}−{n}}\right)^{\frac{{mn}}{{x}}} \\ $$$$=\underset{{t}\rightarrow\infty} {\mathrm{lim}}\left[\left(\frac{{t}+{m}}{{t}−{n}}\right)^{{t}} \right]^{{mn}} \\ $$$$=\underset{{t}\rightarrow\infty} {\mathrm{lim}}\left[\left(\mathrm{1}+\frac{{m}+{n}}{{t}−{n}}\right)^{{t}} \right]^{{mn}} \\ $$$$=\underset{{t}\rightarrow\infty} {\mathrm{lim}}\left[\left(\mathrm{1}+\frac{{m}+{n}}{{t}−{n}}\right)^{{t}−{n}} \left(\mathrm{1}+\frac{{m}+{n}}{{t}−{n}}\right)^{{n}} \right]^{{mn}} \\ $$$$=\underset{{t}\rightarrow\infty} {\mathrm{lim}}\left[\left(\mathrm{1}+\frac{\mathrm{1}}{\frac{{t}−{n}}{{m}+{n}}}\right)^{\frac{{t}−{n}}{{m}+{n}}} \left(\mathrm{1}+\frac{{m}+{n}}{{t}−{n}}\right)^{\frac{{n}}{{m}+{n}}} \right]^{{mn}\left({m}+{n}\right)} \\ $$$$=\left[{e}\left(\mathrm{1}+\mathrm{0}\right)^{\frac{{n}}{{m}+{n}}} \right]^{{mn}\left({m}+{n}\right)} \\ $$$$={e}^{{mn}\left({m}+{n}\right)} \\ $$
Commented by john santu last updated on 03/Feb/20
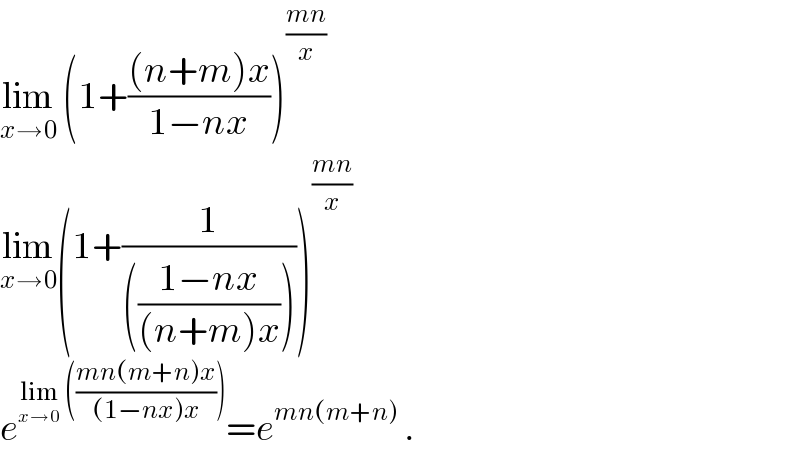
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{1}+\frac{\left({n}+{m}\right){x}}{\mathrm{1}−{nx}}\right)^{\frac{{mn}}{{x}}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{\left(\frac{\mathrm{1}−{nx}}{\left({n}+{m}\right){x}}\right)}\right)^{\frac{{mn}}{{x}}} \\ $$$${e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{{mn}\left({m}+{n}\right){x}}{\left(\mathrm{1}−{nx}\right){x}}\right)} ={e}^{{mn}\left({m}+{n}\right)} \:. \\ $$
Answered by Joel578 last updated on 03/Feb/20
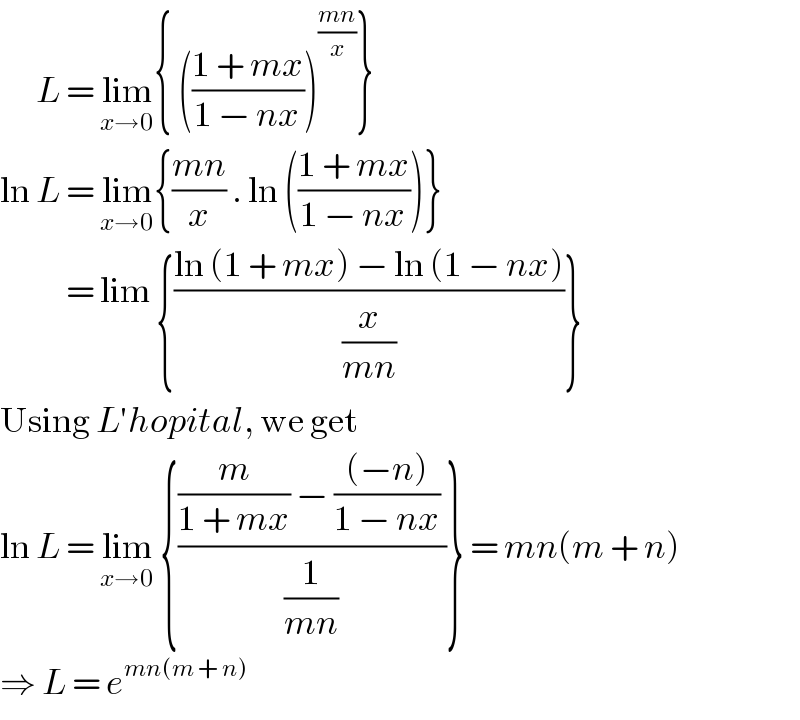
$$\:\:\:\:\:\:{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\:\left(\frac{\mathrm{1}\:+\:{mx}}{\mathrm{1}\:−\:{nx}}\right)^{\frac{{mn}}{{x}}} \right\} \\ $$$$\mathrm{ln}\:{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{{mn}}{{x}}\:.\:\mathrm{ln}\:\left(\frac{\mathrm{1}\:+\:{mx}}{\mathrm{1}\:−\:{nx}}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{lim}\:\left\{\frac{\mathrm{ln}\:\left(\mathrm{1}\:+\:{mx}\right)\:−\:\mathrm{ln}\:\left(\mathrm{1}\:−\:{nx}\right)}{\frac{{x}}{{mn}}}\right\} \\ $$$$\mathrm{Using}\:{L}'{hopital},\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{ln}\:{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left\{\frac{\frac{{m}}{\mathrm{1}\:+\:{mx}}\:−\:\frac{\left(−{n}\right)}{\mathrm{1}\:−\:{nx}}\:}{\frac{\mathrm{1}}{{mn}}}\right\}\:=\:{mn}\left({m}\:+\:{n}\right) \\ $$$$\Rightarrow\:{L}\:=\:{e}^{{mn}\left({m}\:+\:{n}\right)} \\ $$
