Question Number 122236 by benjo_mathlover last updated on 15/Nov/20
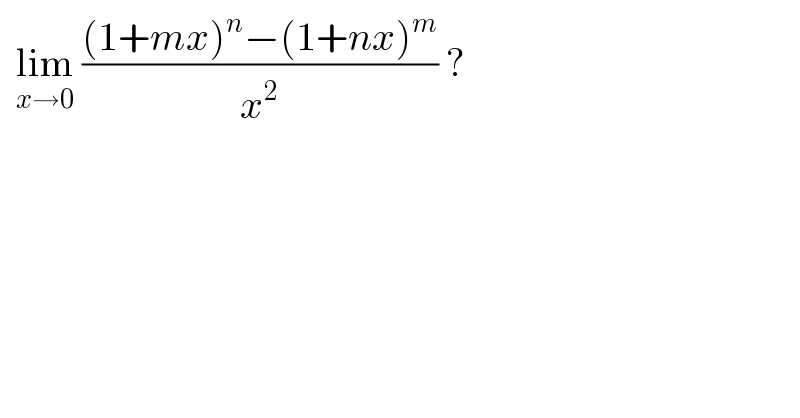
$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+{mx}\right)^{{n}} −\left(\mathrm{1}+{nx}\right)^{{m}} }{{x}^{\mathrm{2}} }\:? \\ $$
Answered by Dwaipayan Shikari last updated on 15/Nov/20
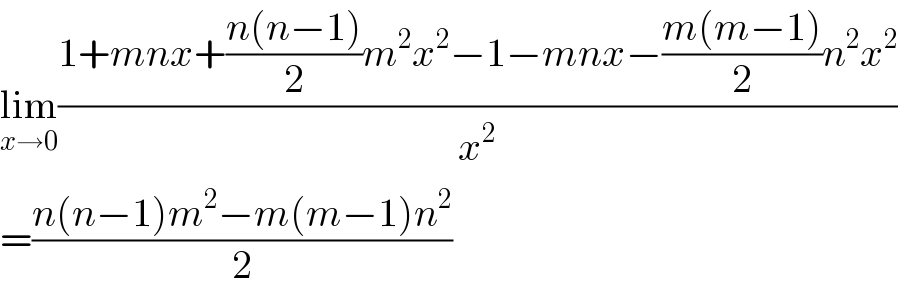
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}+{mnx}+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}{m}^{\mathrm{2}} {x}^{\mathrm{2}} −\mathrm{1}−{mnx}−\frac{{m}\left({m}−\mathrm{1}\right)}{\mathrm{2}}{n}^{\mathrm{2}} {x}^{\mathrm{2}} }{{x}^{\mathrm{2}} } \\ $$$$=\frac{{n}\left({n}−\mathrm{1}\right){m}^{\mathrm{2}} −{m}\left({m}−\mathrm{1}\right){n}^{\mathrm{2}} }{\mathrm{2}} \\ $$
Answered by liberty last updated on 15/Nov/20
![lim_(x→0) ((mn(1+mx)^(n−1) −mn(1+nx)^(m−1) )/(2x)) = ((mn)/2) lim_(x→0) (((1+mx)^(n−1) −(1+nx)^(m−1) )/x) = ((mn)/2) lim_(x→0) ((m(n−1)(1+mx)^(n−2) −n(m−1)(1+nx)^(m−2) )/1) = ((mn)/2) . [ mn−m−mn+n ] = ((mn(n−m))/2).▲](https://www.tinkutara.com/question/Q122239.png)
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{mn}\left(\mathrm{1}+\mathrm{mx}\right)^{\mathrm{n}−\mathrm{1}} −\mathrm{mn}\left(\mathrm{1}+\mathrm{nx}\right)^{\mathrm{m}−\mathrm{1}} }{\mathrm{2x}}\:= \\ $$$$\:\:\frac{\mathrm{mn}}{\mathrm{2}}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\mathrm{mx}\right)^{\mathrm{n}−\mathrm{1}} −\left(\mathrm{1}+\mathrm{nx}\right)^{\mathrm{m}−\mathrm{1}} }{\mathrm{x}}\:= \\ $$$$\frac{\mathrm{mn}}{\mathrm{2}}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{m}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{1}+\mathrm{mx}\right)^{\mathrm{n}−\mathrm{2}} −\mathrm{n}\left(\mathrm{m}−\mathrm{1}\right)\left(\mathrm{1}+\mathrm{nx}\right)^{\mathrm{m}−\mathrm{2}} }{\mathrm{1}}\:= \\ $$$$\:\frac{\mathrm{mn}}{\mathrm{2}}\:.\:\left[\:\mathrm{mn}−\mathrm{m}−\mathrm{mn}+\mathrm{n}\:\right]\:=\:\frac{\mathrm{mn}\left(\mathrm{n}−\mathrm{m}\right)}{\mathrm{2}}.\blacktriangle \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 15/Nov/20
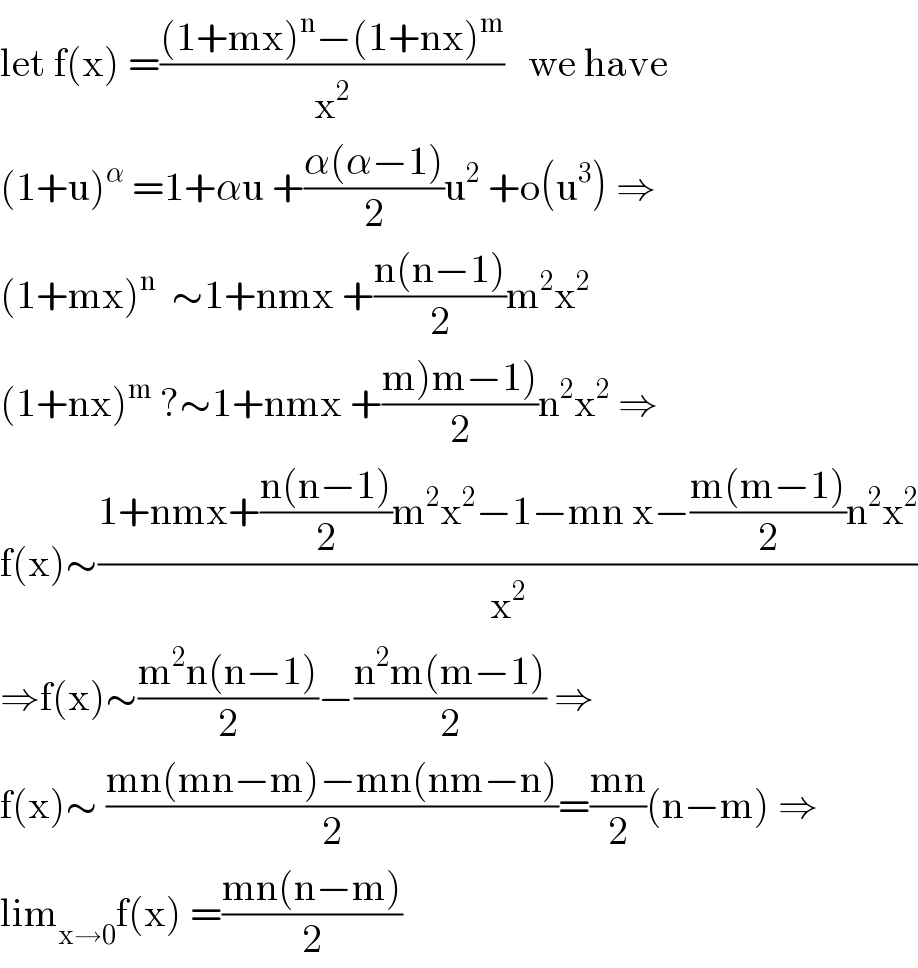
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\left(\mathrm{1}+\mathrm{mx}\right)^{\mathrm{n}} −\left(\mathrm{1}+\mathrm{nx}\right)^{\mathrm{m}} }{\mathrm{x}^{\mathrm{2}} }\:\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\left(\mathrm{1}+\mathrm{u}\right)^{\alpha} \:=\mathrm{1}+\alpha\mathrm{u}\:+\frac{\alpha\left(\alpha−\mathrm{1}\right)}{\mathrm{2}}\mathrm{u}^{\mathrm{2}} \:+\mathrm{o}\left(\mathrm{u}^{\mathrm{3}} \right)\:\Rightarrow \\ $$$$\left(\mathrm{1}+\mathrm{mx}\right)^{\mathrm{n}} \:\:\sim\mathrm{1}+\mathrm{nmx}\:+\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)}{\mathrm{2}}\mathrm{m}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+\mathrm{nx}\right)^{\mathrm{m}} \:?\sim\mathrm{1}+\mathrm{nmx}\:+\frac{\left.\mathrm{m}\left.\right)\mathrm{m}−\mathrm{1}\right)}{\mathrm{2}}\mathrm{n}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{1}+\mathrm{nmx}+\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)}{\mathrm{2}}\mathrm{m}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{1}−\mathrm{mn}\:\mathrm{x}−\frac{\mathrm{m}\left(\mathrm{m}−\mathrm{1}\right)}{\mathrm{2}}\mathrm{n}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{m}^{\mathrm{2}} \mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)}{\mathrm{2}}−\frac{\mathrm{n}^{\mathrm{2}} \mathrm{m}\left(\mathrm{m}−\mathrm{1}\right)}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\sim\:\frac{\mathrm{mn}\left(\mathrm{mn}−\mathrm{m}\right)−\mathrm{mn}\left(\mathrm{nm}−\mathrm{n}\right)}{\mathrm{2}}=\frac{\mathrm{mn}}{\mathrm{2}}\left(\mathrm{n}−\mathrm{m}\right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{mn}\left(\mathrm{n}−\mathrm{m}\right)}{\mathrm{2}} \\ $$
