Question Number 170166 by sciencestudent last updated on 17/May/22
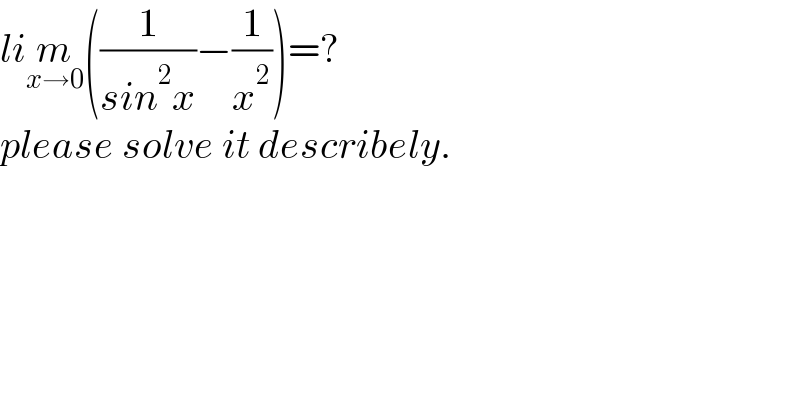
$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\left(\frac{\mathrm{1}}{{sin}^{\mathrm{2}} {x}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)=? \\ $$$${please}\:{solve}\:{it}\:{describely}. \\ $$
Commented by mr W last updated on 17/May/22

$${it}\:{is}\:{solved}\:{descriptively}\:{enough}! \\ $$$${if}\:{you}\:{don}'{t}\:{understand}\:{something}, \\ $$$${you}\:{can}\:{tell}\:{what}\:{you}\:{don}'{t}\: \\ $$$${understand},\:{instead}\:{of}\:{posting}\:{the} \\ $$$${same}\:{question}\:{again}\:{and}\:{again}. \\ $$
Answered by ajfour last updated on 17/May/22

$${consider}\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:{aplpied}\:{on} \\ $$$${both}\:{sides}\:{of}\:{steps}\:{that}\:{follow} \\ $$$$\left({Lx}^{\mathrm{2}} +\mathrm{1}\right)=\left(\frac{{x}}{\mathrm{sin}\:{x}}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{Lx}=\mathrm{2}\left(\frac{{x}}{\mathrm{sin}\:{x}}\right)\left(\frac{\mathrm{sin}\:{x}−{x}\mathrm{cos}\:{x}}{\mathrm{sin}\:^{\mathrm{2}} {x}}\right) \\ $$$${L}=\frac{\mathrm{sin}\:{x}−{x}\mathrm{cos}\:{x}}{\mathrm{sin}\:^{\mathrm{3}} {x}} \\ $$$$\:\:\:\:=\frac{\mathrm{cos}\:{x}−\left(\mathrm{cos}\:{x}−{x}\mathrm{sin}\:{x}\right)}{\mathrm{3sin}\:^{\mathrm{2}} {x}} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{{x}}{\mathrm{sin}\:{x}}\right)\:\:=\frac{\mathrm{1}}{\mathrm{3}} \\ $$
