Question Number 91419 by john santu last updated on 30/Apr/20
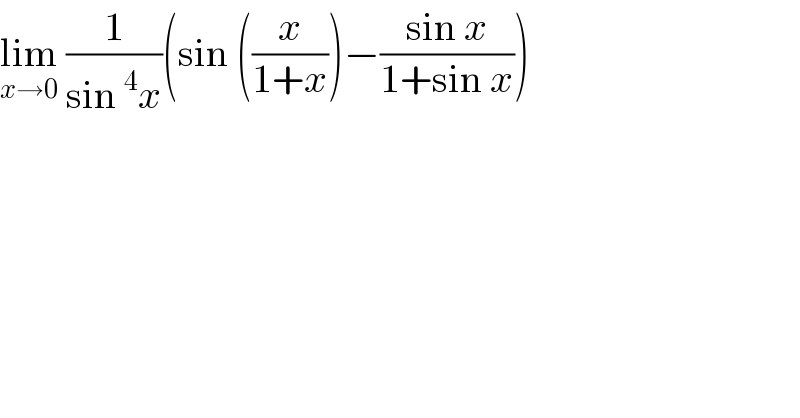
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{4}} {x}}\left(\mathrm{sin}\:\left(\frac{{x}}{\mathrm{1}+{x}}\right)−\frac{\mathrm{sin}\:{x}}{\mathrm{1}+\mathrm{sin}\:{x}}\right) \\ $$
Commented by john santu last updated on 01/May/20

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{4}} {x}}\:\left(\frac{\left(\mathrm{1}+\mathrm{sin}\:{x}\right)\mathrm{sin}\:\left(\frac{{x}}{\mathrm{1}+{x}}\right)−\mathrm{sin}\:{x}}{\mathrm{1}+\mathrm{sin}\:{x}}\right)\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\frac{{x}}{\mathrm{1}+{x}}\right)+\mathrm{sin}\:{x}\:\mathrm{sin}\:\left(\frac{{x}}{\mathrm{1}+{x}}\right)−\mathrm{sin}\:{x}}{\mathrm{sin}\:^{\mathrm{4}} {x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}\:\mathrm{sin}\:\left(\frac{{x}}{\mathrm{1}+{x}}\right)+\left(\mathrm{2cos}\:\left(\frac{{x}\left({x}+\mathrm{2}\right)}{\mathrm{2}\left({x}+\mathrm{1}\right)}\right)\:\mathrm{sin}\:\left(\frac{−{x}^{\mathrm{2}} }{\mathrm{2}\left({x}+\mathrm{1}\right)}\right)\right.}{\mathrm{sin}\:^{\mathrm{4}} {x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}}\:−\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}}}{{x}^{\mathrm{4}} }\:=\:\mathrm{0} \\ $$
