Question Number 144645 by mathdanisur last updated on 27/Jun/21
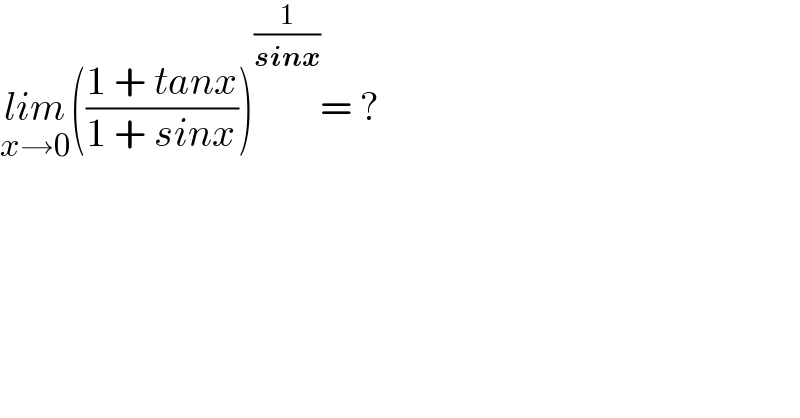
$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\left(\frac{\mathrm{1}\:+\:{tanx}}{\mathrm{1}\:+\:{sinx}}\right)^{\frac{\mathrm{1}}{\boldsymbol{{sinx}}}} =\:? \\ $$
Answered by liberty last updated on 27/Jun/21
![lim_(x→0) (((1+sin x+tan x−sin x)/(1+sin x)))^(1/(sin x)) = lim_(x→0) (1+((tan x−sin x)/(1+sin x)))^(1/(sin x)) = lim_(x→0) [(1+((tan x−sin x)/(1+sin x)))^((1+sin x)/(tan x−sin x)) ]^((tan x−sin x)/(sin x(1+sin x))) =e^(lim_(x→0) (((tan x−sin x)/(sin x(1+sin x))))) = e^(lim_(x→0) (((tan x(1−cos x))/(sin x(1+sin x))))) = e^(0/1) = e^0 = 1.](https://www.tinkutara.com/question/Q144650.png)
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}+\mathrm{sin}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{x}}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{tan}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{x}}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\mathrm{1}+\frac{\mathrm{tan}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}\right)^{\frac{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}{\mathrm{tan}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}}} \right]^{\frac{\mathrm{tan}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{x}\right)}} \\ $$$$=\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{tan}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{x}\right)}\right)} \\ $$$$=\:\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{tan}\:\mathrm{x}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{x}\right)}{\mathrm{sin}\:\mathrm{x}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{x}\right)}\right)} \\ $$$$=\:\mathrm{e}^{\frac{\mathrm{0}}{\mathrm{1}}} =\:\mathrm{e}^{\mathrm{0}} \:=\:\mathrm{1}. \\ $$
Commented by mathdanisur last updated on 27/Jun/21
$${alot}\:{cool}\:{thank}\:{you}\:{Sir} \\ $$
Answered by mathmax by abdo last updated on 27/Jun/21
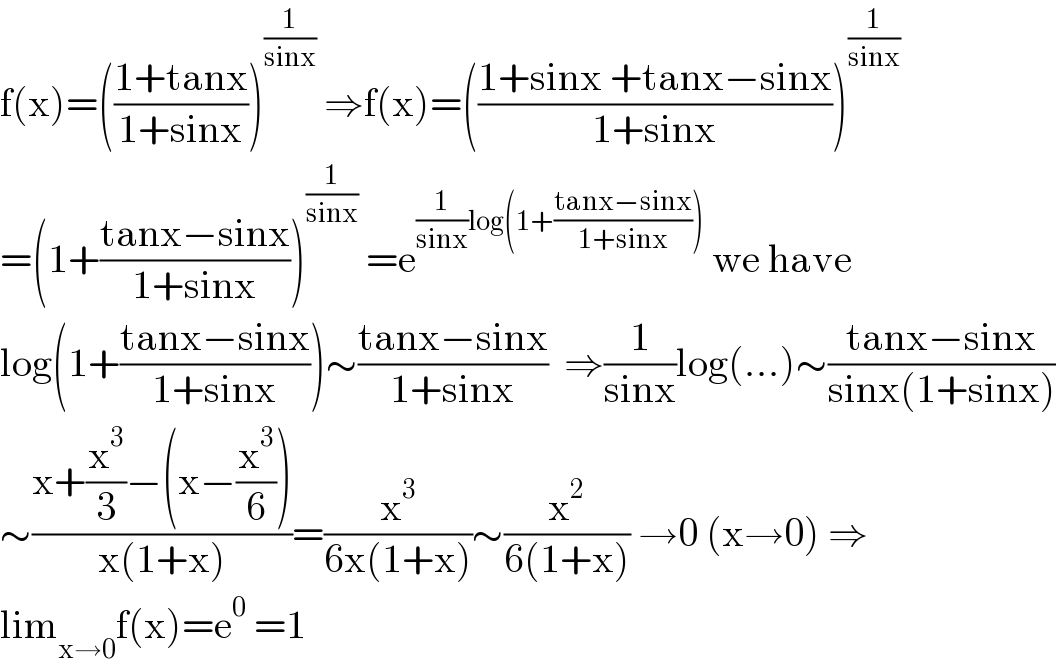
$$\mathrm{f}\left(\mathrm{x}\right)=\left(\frac{\mathrm{1}+\mathrm{tanx}}{\mathrm{1}+\mathrm{sinx}}\right)^{\frac{\mathrm{1}}{\mathrm{sinx}}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\left(\frac{\mathrm{1}+\mathrm{sinx}\:+\mathrm{tanx}−\mathrm{sinx}}{\mathrm{1}+\mathrm{sinx}}\right)^{\frac{\mathrm{1}}{\mathrm{sinx}}} \\ $$$$=\left(\mathrm{1}+\frac{\mathrm{tanx}−\mathrm{sinx}}{\mathrm{1}+\mathrm{sinx}}\right)^{\frac{\mathrm{1}}{\mathrm{sinx}}} \:=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{sinx}}\mathrm{log}\left(\mathrm{1}+\frac{\mathrm{tanx}−\mathrm{sinx}}{\mathrm{1}+\mathrm{sinx}}\right)} \:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{log}\left(\mathrm{1}+\frac{\mathrm{tanx}−\mathrm{sinx}}{\mathrm{1}+\mathrm{sinx}}\right)\sim\frac{\mathrm{tanx}−\mathrm{sinx}}{\mathrm{1}+\mathrm{sinx}}\:\:\Rightarrow\frac{\mathrm{1}}{\mathrm{sinx}}\mathrm{log}\left(…\right)\sim\frac{\mathrm{tanx}−\mathrm{sinx}}{\mathrm{sinx}\left(\mathrm{1}+\mathrm{sinx}\right)} \\ $$$$\sim\frac{\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}−\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\right)}{\mathrm{x}\left(\mathrm{1}+\mathrm{x}\right)}=\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6x}\left(\mathrm{1}+\mathrm{x}\right)}\sim\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}\left(\mathrm{1}+\mathrm{x}\right)}\:\rightarrow\mathrm{0}\:\left(\mathrm{x}\rightarrow\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{\mathrm{0}} \:=\mathrm{1} \\ $$
Commented by mathdanisur last updated on 27/Jun/21
$${Thanks}\:{Sir}\:{alot}\:{cool} \\ $$
