Question Number 28095 by tawa tawa last updated on 20/Jan/18
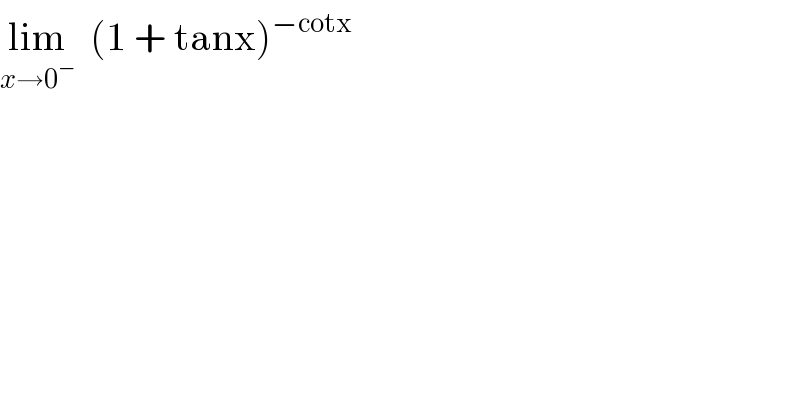
$$\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\:\left(\mathrm{1}\:+\:\mathrm{tanx}\right)^{−\mathrm{cotx}} \\ $$
Commented by abdo imad last updated on 20/Jan/18
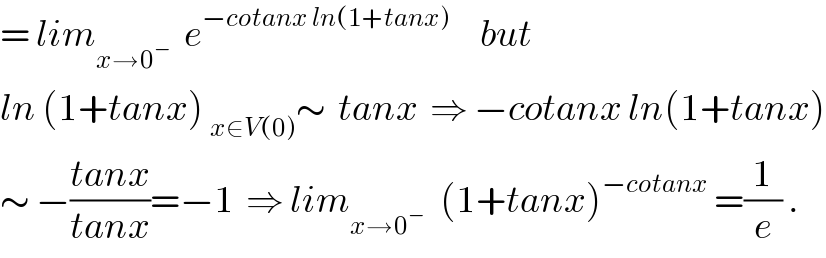
$$=\:{lim}_{{x}\rightarrow\mathrm{0}^{−} } \:\:{e}^{−{cotanx}\:{ln}\left(\mathrm{1}+{tanx}\right)} \:\:\:\:\:{but}\: \\ $$$${ln}\:\left(\mathrm{1}+{tanx}\right)\:_{{x}\in{V}\left(\mathrm{0}\right)} \sim\:\:{tanx}\:\:\Rightarrow\:−{cotanx}\:{ln}\left(\mathrm{1}+{tanx}\right) \\ $$$$\sim\:−\frac{{tanx}}{{tanx}}=−\mathrm{1}\:\:\Rightarrow\:{lim}_{{x}\rightarrow\mathrm{0}^{−\:} } \:\:\left(\mathrm{1}+{tanx}\right)^{−{cotanx}} \:=\frac{\mathrm{1}}{{e}}\:. \\ $$
Commented by tawa tawa last updated on 21/Jan/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
