Question Number 85293 by jagoll last updated on 20/Mar/20
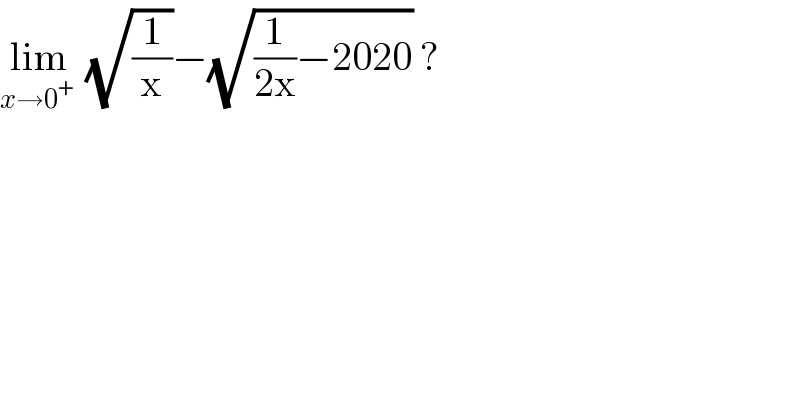
$$\underset{{x}\rightarrow\mathrm{0}^{+} \:} {\mathrm{lim}}\:\sqrt{\frac{\mathrm{1}}{\mathrm{x}}}−\sqrt{\frac{\mathrm{1}}{\mathrm{2x}}−\mathrm{2020}}\:? \\ $$
Commented by jagoll last updated on 20/Mar/20
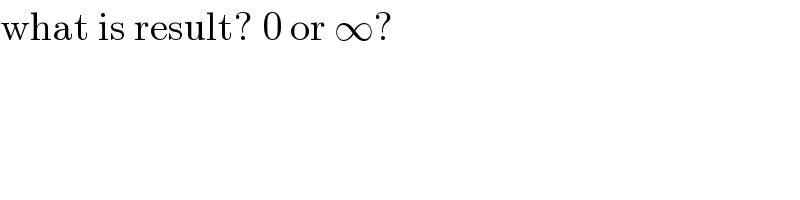
$$\mathrm{what}\:\mathrm{is}\:\mathrm{result}?\:\mathrm{0}\:\mathrm{or}\:\infty? \\ $$
Answered by mr W last updated on 20/Mar/20
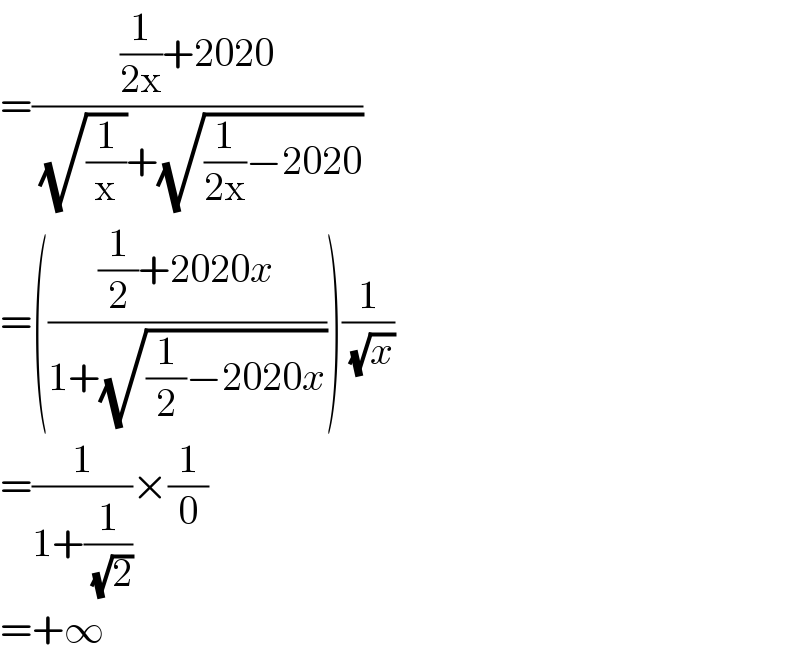
$$=\frac{\frac{\mathrm{1}}{\mathrm{2x}}+\mathrm{2020}}{\:\sqrt{\frac{\mathrm{1}}{\mathrm{x}}}+\sqrt{\frac{\mathrm{1}}{\mathrm{2x}}−\mathrm{2020}}} \\ $$$$=\left(\frac{\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2020}{x}}{\mathrm{1}+\sqrt{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2020}{x}}}\right)\frac{\mathrm{1}}{\:\sqrt{{x}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}×\frac{\mathrm{1}}{\mathrm{0}} \\ $$$$=+\infty \\ $$
Commented by jagoll last updated on 20/Mar/20
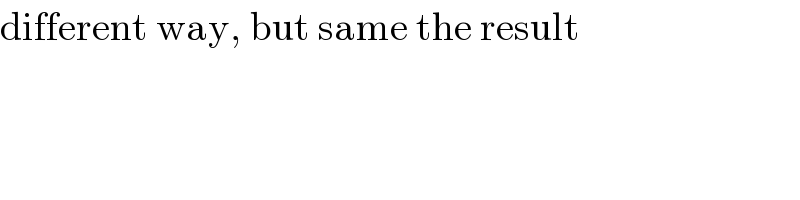
$$\mathrm{different}\:\mathrm{way},\:\mathrm{but}\:\mathrm{same}\:\mathrm{the}\:\mathrm{result} \\ $$
Answered by jagoll last updated on 20/Mar/20
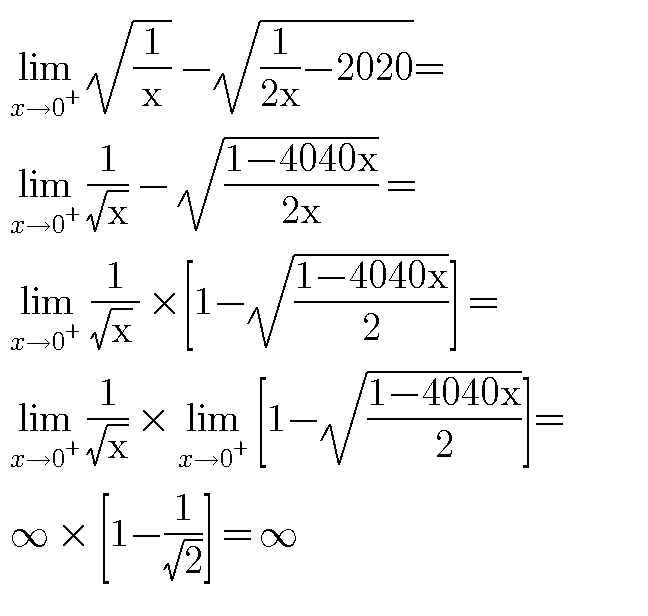
Commented by prakash jain last updated on 20/Mar/20
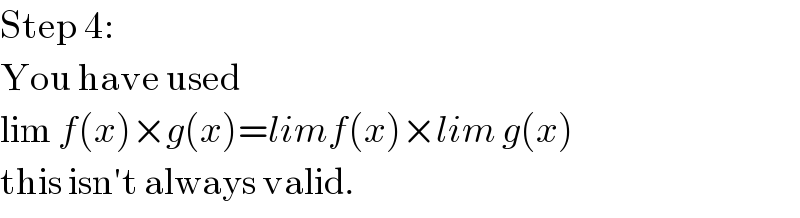
$$\mathrm{Step}\:\mathrm{4}: \\ $$$$\mathrm{You}\:\mathrm{have}\:\mathrm{used}\: \\ $$$$\mathrm{lim}\:{f}\left({x}\right)×{g}\left({x}\right)={limf}\left({x}\right)×{lim}\:{g}\left({x}\right) \\ $$$$\mathrm{this}\:\mathrm{isn}'\mathrm{t}\:\mathrm{always}\:\mathrm{valid}. \\ $$
