Question Number 88098 by ar247 last updated on 08/Apr/20
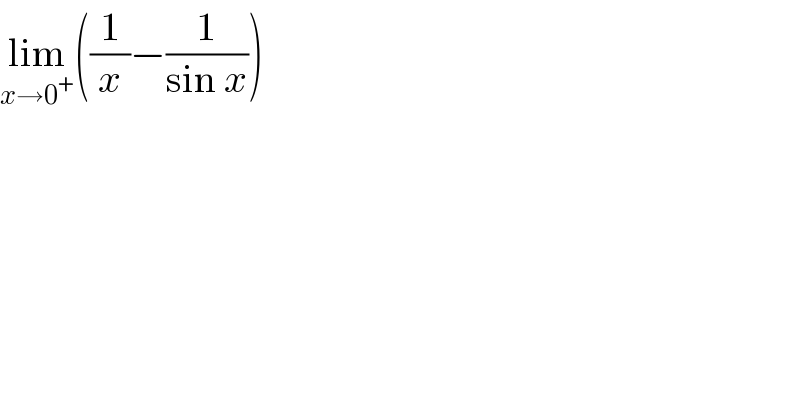
$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{sin}\:{x}}\right) \\ $$
Commented by ar247 last updated on 08/Apr/20
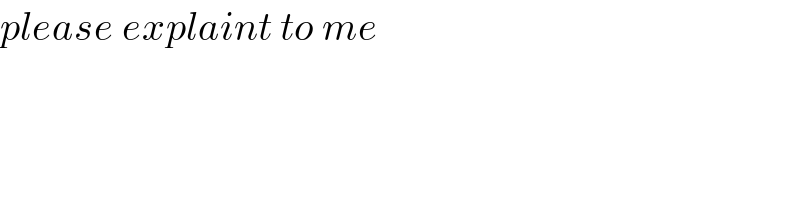
$${please}\:{explaint}\:{to}\:{me} \\ $$
Commented by mathmax by abdo last updated on 08/Apr/20
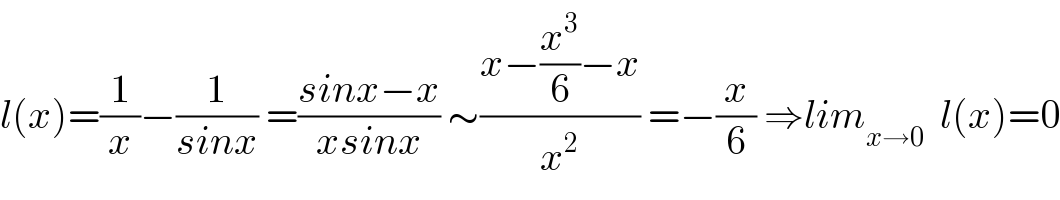
$${l}\left({x}\right)=\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{sinx}}\:=\frac{{sinx}−{x}}{{xsinx}}\:\sim\frac{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}−{x}}{{x}^{\mathrm{2}} }\:=−\frac{{x}}{\mathrm{6}}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:{l}\left({x}\right)=\mathrm{0} \\ $$
