Question Number 122835 by liberty last updated on 20/Nov/20
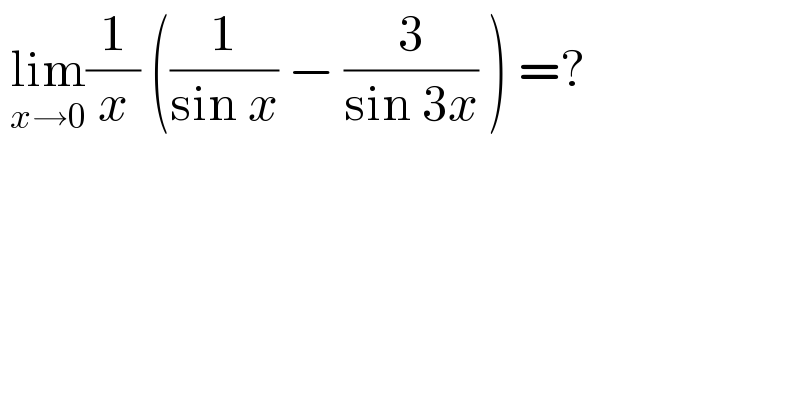
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}\:\left(\frac{\mathrm{1}}{\mathrm{sin}\:{x}}\:−\:\frac{\mathrm{3}}{\mathrm{sin}\:\mathrm{3}{x}}\:\right)\:=? \\ $$
Answered by $@y@m last updated on 20/Nov/20
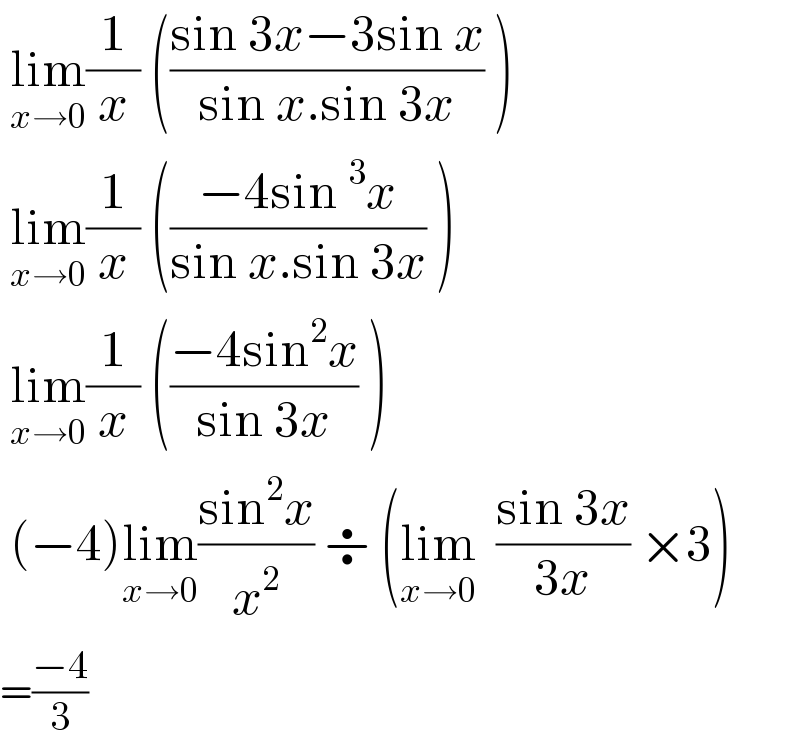
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}\:\left(\frac{\mathrm{sin}\:\mathrm{3}{x}−\mathrm{3sin}\:{x}}{\mathrm{sin}\:{x}.\mathrm{sin}\:\mathrm{3}{x}}\:\right)\: \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}\:\left(\frac{−\mathrm{4sin}\:^{\mathrm{3}} {x}}{\mathrm{sin}\:{x}.\mathrm{sin}\:\mathrm{3}{x}}\:\right)\: \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}\:\left(\frac{−\mathrm{4sin}^{\mathrm{2}} {x}}{\mathrm{sin}\:\mathrm{3}{x}}\:\right)\: \\ $$$$\:\left(−\mathrm{4}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }\:\boldsymbol{\div}\:\left(\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{3}{x}}\:×\mathrm{3}\right)\: \\ $$$$=\frac{−\mathrm{4}}{\mathrm{3}} \\ $$
