Menu Close

lim-x-0-1-x-1-x-2-2-cos-x-1-

Tinku Tara 0 Comments
Pin




Question Number 90722 by jagoll last updated on 25/Apr/20
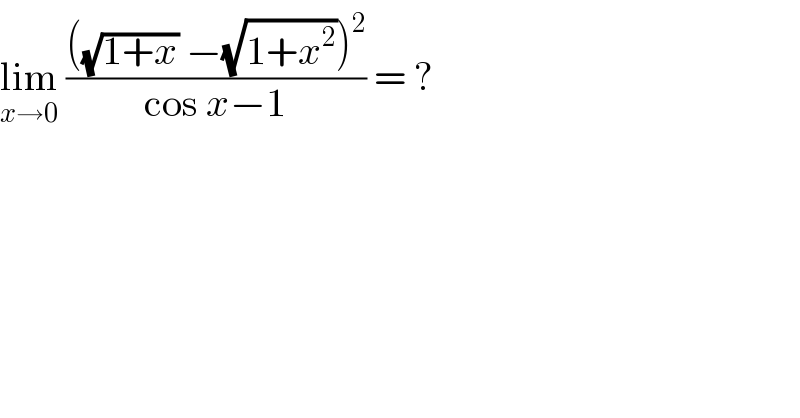
lim_(x→0) ((((√(1+x)) −(√(1+x^2 )))^2 )/(cos x−1)) = ?
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\sqrt{\mathrm{1}+{x}}\:−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }{\mathrm{cos}\:{x}−\mathrm{1}}\:=\:? \\ $$
Commented by john santu last updated on 25/Apr/20
lim_(x→0) ((((√(1+x))−(√(1+x^2 )))^2 )/(−2sin^2 ((1/2)x) )) −(1/2) [ lim_(x→0) (((√(1+x))−(√(1+x^2 )))/(sin ((x/2)))) ]^2 −(1/2)[ lim_(x→0) (((1+(x/2))−(1+(x^2 /2)))/(((x/2))))]^2 −(1/2) [lim_(x→0) ((((x/2)){1−x})/(((x/2)))) ]^2 = −(1/2)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\sqrt{\mathrm{1}+{x}}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }{−\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}{x}\right)\:} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\:\left[\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}+{x}}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\mathrm{sin}\:\left(\frac{{x}}{\mathrm{2}}\right)}\:\right]^{\mathrm{2}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\left[\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\frac{{x}}{\mathrm{2}}\right)−\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)}{\left(\frac{{x}}{\mathrm{2}}\right)}\right]^{\mathrm{2}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\:\left[\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\frac{{x}}{\mathrm{2}}\right)\left\{\mathrm{1}−{x}\right\}}{\left(\frac{{x}}{\mathrm{2}}\right)}\:\right]^{\mathrm{2}} \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 25/Apr/20
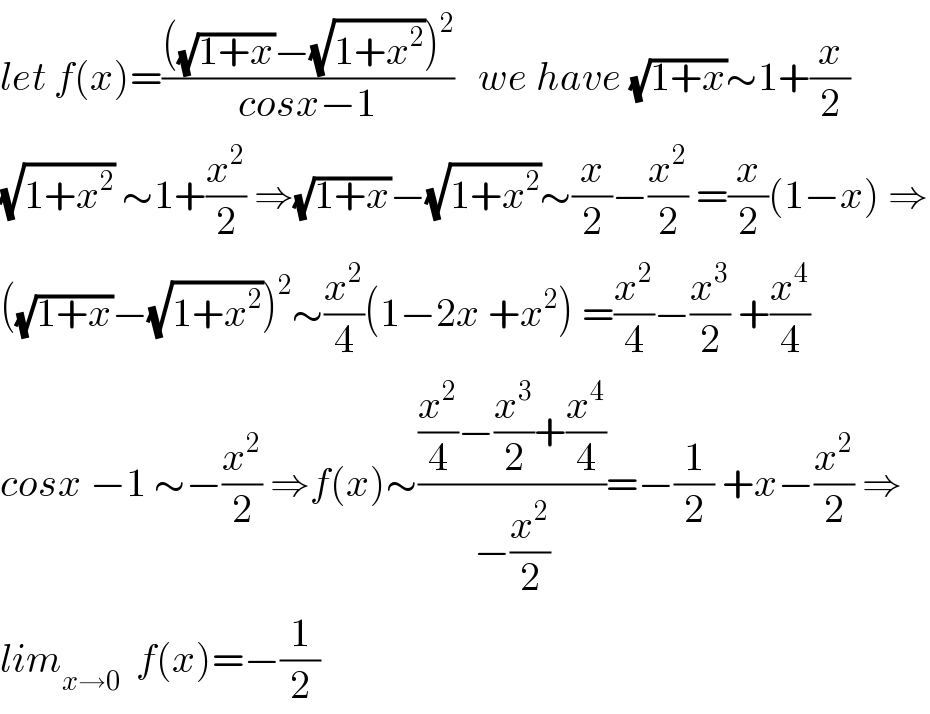
let f(x)=((((√(1+x))−(√(1+x^2 )))^2 )/(cosx−1)) we have (√(1+x))∼1+(x/2) (√(1+x^2 )) ∼1+(x^2 /2) ⇒(√(1+x))−(√(1+x^2 ))∼(x/2)−(x^2 /2) =(x/2)(1−x) ⇒ ((√(1+x))−(√(1+x^2 )))^2 ∼(x^2 /4)(1−2x +x^2 ) =(x^2 /4)−(x^3 /2) +(x^4 /4) cosx −1 ∼−(x^2 /2) ⇒f(x)∼(((x^2 /4)−(x^3 /2)+(x^4 /4))/(−(x^2 /2)))=−(1/2) +x−(x^2 /2) ⇒ lim_(x→0) f(x)=−(1/2)
$${let}\:{f}\left({x}\right)=\frac{\left(\sqrt{\mathrm{1}+{x}}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }{{cosx}−\mathrm{1}}\:\:\:{we}\:{have}\:\sqrt{\mathrm{1}+{x}}\sim\mathrm{1}+\frac{{x}}{\mathrm{2}} \\ $$$$\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\sim\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\sqrt{\mathrm{1}+{x}}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\sim\frac{{x}}{\mathrm{2}}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:=\frac{{x}}{\mathrm{2}}\left(\mathrm{1}−{x}\right)\:\Rightarrow \\ $$$$\left(\sqrt{\mathrm{1}+{x}}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \sim\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{1}−\mathrm{2}{x}\:+{x}^{\mathrm{2}} \right)\:=\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−\frac{{x}^{\mathrm{3}} }{\mathrm{2}}\:+\frac{{x}^{\mathrm{4}} }{\mathrm{4}} \\ $$$${cosx}\:−\mathrm{1}\:\sim−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow{f}\left({x}\right)\sim\frac{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−\frac{{x}^{\mathrm{3}} }{\mathrm{2}}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}}}{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}=−\frac{\mathrm{1}}{\mathrm{2}}\:+{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:{f}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by jagoll last updated on 25/Apr/20
thank you all
$${thank}\:{you}\:{all} \\ $$
Answered by TANMAY PANACEA. last updated on 25/Apr/20
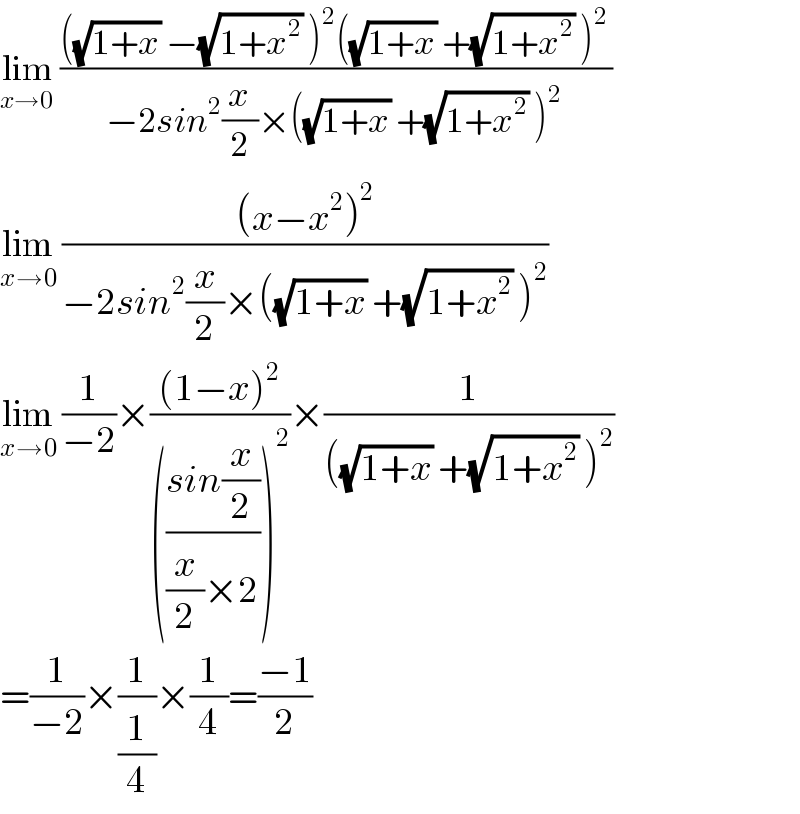
lim_(x→0) ((((√(1+x)) −(√(1+x^2 )) )^2 ((√(1+x)) +(√(1+x^2 )) )^2 )/(−2sin^2 (x/2)×((√(1+x)) +(√(1+x^2 )) )^2 )) lim_(x→0) (((x−x^2 )^2 )/(−2sin^2 (x/2)×((√(1+x)) +(√(1+x^2 )) )^2 )) lim_(x→0) (1/(−2))×(((1−x)^2 )/((((sin(x/2))/((x/2)×2)))^2 ))×(1/(((√(1+x)) +(√(1+x^2 )) )^2 )) =(1/(−2))×(1/(1/4))×(1/4)=((−1)/2)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\sqrt{\mathrm{1}+{x}}\:−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right)^{\mathrm{2}} \left(\sqrt{\mathrm{1}+{x}}\:+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right)^{\mathrm{2}} }{−\mathrm{2}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}×\left(\sqrt{\mathrm{1}+{x}}\:+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right)^{\mathrm{2}} }\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left({x}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{−\mathrm{2}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}×\left(\sqrt{\mathrm{1}+{x}}\:+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right)^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{−\mathrm{2}}×\frac{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }{\left(\frac{{sin}\frac{{x}}{\mathrm{2}}}{\frac{{x}}{\mathrm{2}}×\mathrm{2}}\right)^{\mathrm{2}} }×\frac{\mathrm{1}}{\left(\sqrt{\mathrm{1}+{x}}\:+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{−\mathrm{2}}×\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{4}}}×\frac{\mathrm{1}}{\mathrm{4}}=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$
Commented by peter frank last updated on 25/Apr/20
thank you both
$${thank}\:{you}\:{both} \\ $$
Commented by peter frank last updated on 26/Apr/20
help 90341
$${help}\:\mathrm{90341} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *