Question Number 152211 by nitu last updated on 26/Aug/21

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{should}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{be}\:\infty\:\mathrm{or}\:\mathrm{is}\:\mathrm{it}\:\mathrm{DNE}. \\ $$$$\mathrm{my}\:\mathrm{main}\:\mathrm{question}\:\mathrm{is}, \\ $$$$\mathrm{when}, \\ $$$$\underset{{x}\rightarrow\mathrm{a}} {\mathrm{lim}}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\infty\: \\ $$$$\mathrm{does}\:\mathrm{it}\:\mathrm{not}\:\mathrm{exist}?\:\mathrm{is}\:\mathrm{it}\:\mathrm{DNE}? \\ $$
Commented by MJS_new last updated on 26/Aug/21
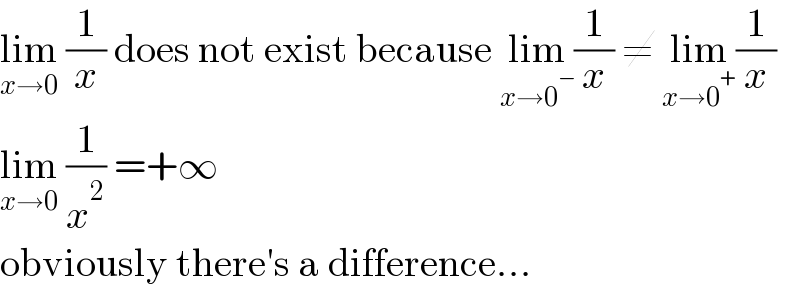
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{x}}\:\mathrm{does}\:\mathrm{not}\:\mathrm{exist}\:\mathrm{because}\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\frac{\mathrm{1}}{{x}}\:\neq\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\mathrm{1}}{{x}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:=+\infty \\ $$$$\mathrm{obviously}\:\mathrm{there}'\mathrm{s}\:\mathrm{a}\:\mathrm{difference}… \\ $$
