Question Number 162925 by qaz last updated on 02/Jan/22
![lim_(x→0) (1/x^4 )[(1+x+(x^2 /2)+(x^3 /3))^(1/(x+(x^2 /2)+(x^3 /3))) −(1+x+(x^2 /2)+(x^3 /3)+(x^4 /4))^(1/(x+(x^2 /2)+(x^3 /3)+(x^4 /4))) ]=?](https://www.tinkutara.com/question/Q162925.png)
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} }\left[\left(\mathrm{1}+\mathrm{x}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{x}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}}} −\left(\mathrm{1}+\mathrm{x}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}}\right)^{\frac{\mathrm{1}}{\mathrm{x}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}}}} \right]=? \\ $$
Answered by Ar Brandon last updated on 02/Jan/22
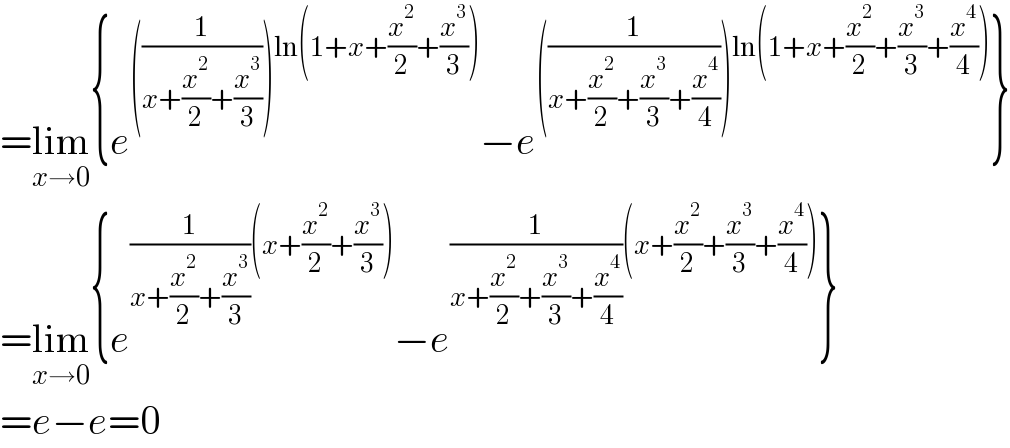
$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{{e}^{\left(\frac{\mathrm{1}}{{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}}\right)\mathrm{ln}\left(\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)} −{e}^{\left(\frac{\mathrm{1}}{{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}}}\right)\mathrm{ln}\left(\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\right)} \right\} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{{e}^{\frac{\mathrm{1}}{{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}}\left({x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)} −{e}^{\frac{\mathrm{1}}{{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}}}\left({x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\right)} \right\} \\ $$$$={e}−{e}=\mathrm{0} \\ $$
Commented by qaz last updated on 02/Jan/22

$$\mathrm{what}'\mathrm{s}\:\mathrm{about}\:\mathrm{Q162926}\:? \\ $$
Commented by qaz last updated on 02/Jan/22

$$\mathrm{sorry}\:.\mathrm{I}\:\mathrm{typed}\:\mathrm{wrong} \\ $$
Commented by Ar Brandon last updated on 02/Jan/22

$$\frac{{e}}{\mathrm{8}} \\ $$
