Question Number 99936 by student work last updated on 24/Jun/20
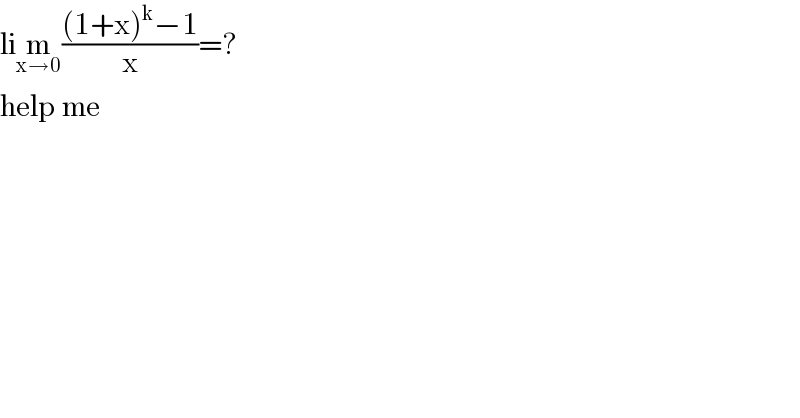
$$\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{m}}\frac{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{k}} −\mathrm{1}}{\mathrm{x}}=? \\ $$$$\mathrm{help}\:\mathrm{me} \\ $$
Commented by bemath last updated on 24/Jun/20
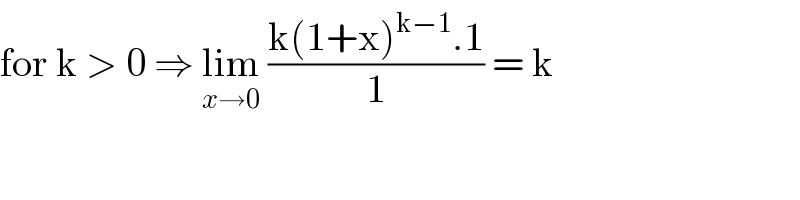
$$\mathrm{for}\:\mathrm{k}\:>\:\mathrm{0}\:\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{k}\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{k}−\mathrm{1}} .\mathrm{1}}{\mathrm{1}}\:=\:\mathrm{k} \\ $$
Commented by Dwaipayan Shikari last updated on 24/Jun/20
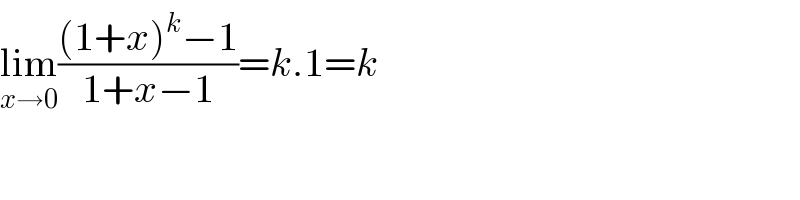
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+{x}\right)^{{k}} −\mathrm{1}}{\mathrm{1}+{x}−\mathrm{1}}={k}.\mathrm{1}={k} \\ $$
Commented by Dwaipayan Shikari last updated on 24/Jun/20

$${k} \\ $$
Answered by mathmax by abdo last updated on 24/Jun/20
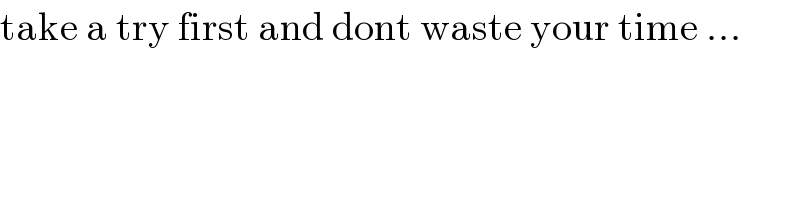
$$\mathrm{take}\:\mathrm{a}\:\mathrm{try}\:\mathrm{first}\:\mathrm{and}\:\mathrm{dont}\:\mathrm{waste}\:\mathrm{your}\:\mathrm{time}\:… \\ $$
Answered by mathmax by abdo last updated on 24/Jun/20
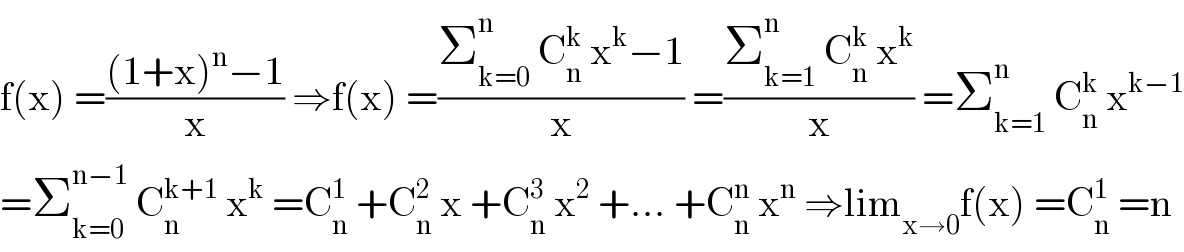
$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{n}} −\mathrm{1}}{\mathrm{x}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}} −\mathrm{1}}{\mathrm{x}}\:=\frac{\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}} }{\mathrm{x}}\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}−\mathrm{1}} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}+\mathrm{1}} \:\mathrm{x}^{\mathrm{k}} \:=\mathrm{C}_{\mathrm{n}} ^{\mathrm{1}} \:+\mathrm{C}_{\mathrm{n}} ^{\mathrm{2}} \:\mathrm{x}\:+\mathrm{C}_{\mathrm{n}} ^{\mathrm{3}} \:\mathrm{x}^{\mathrm{2}} \:+…\:+\mathrm{C}_{\mathrm{n}} ^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}} \:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{C}_{\mathrm{n}} ^{\mathrm{1}} \:=\mathrm{n} \\ $$
