Question Number 116417 by bemath last updated on 03/Oct/20
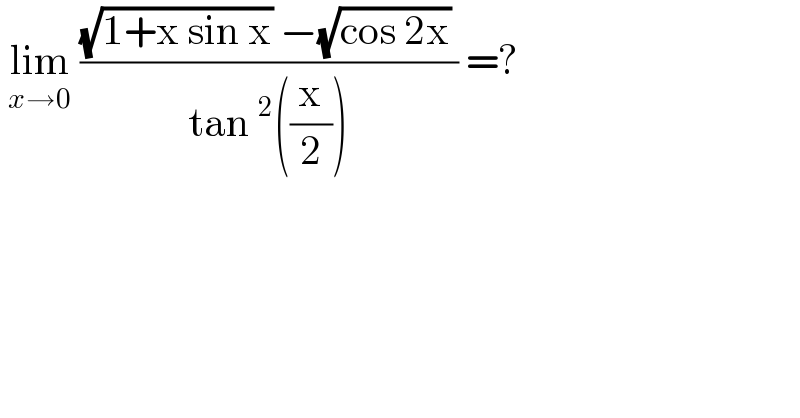
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}+\mathrm{x}\:\mathrm{sin}\:\mathrm{x}}\:−\sqrt{\mathrm{cos}\:\mathrm{2x}}\:}{\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)}\:=? \\ $$
Answered by Bird last updated on 03/Oct/20
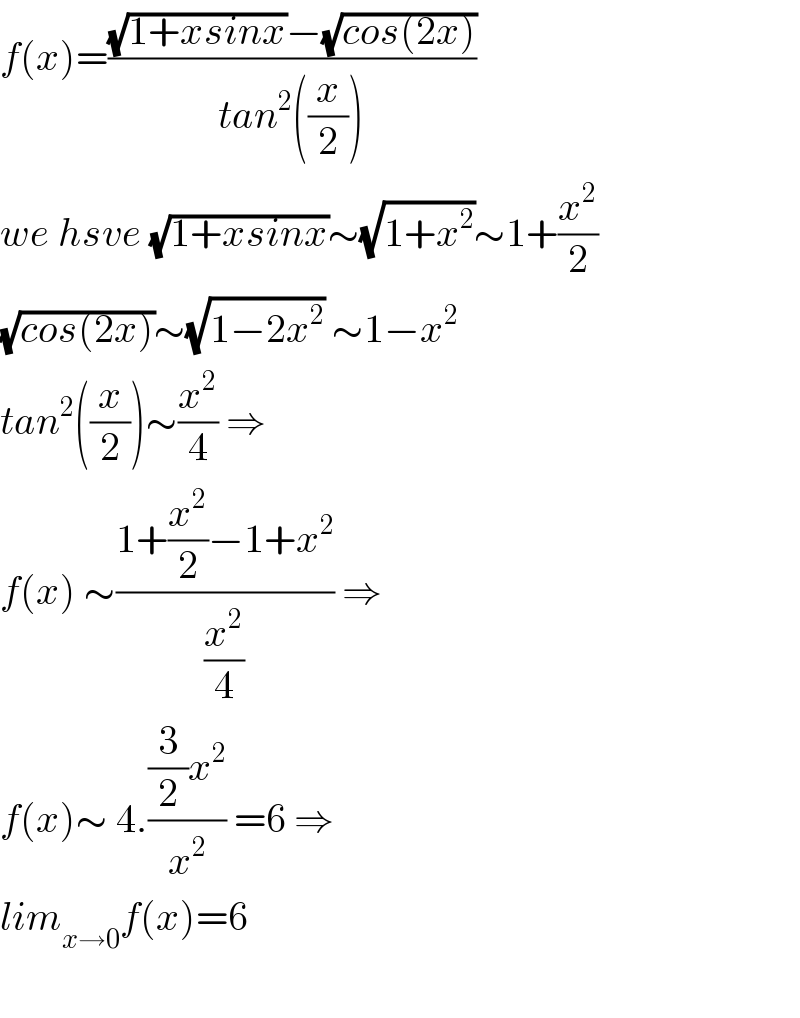
$${f}\left({x}\right)=\frac{\sqrt{\mathrm{1}+{xsinx}}−\sqrt{{cos}\left(\mathrm{2}{x}\right)}}{{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$${we}\:{hsve}\:\sqrt{\mathrm{1}+{xsinx}}\sim\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\sim\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\sqrt{{cos}\left(\mathrm{2}{x}\right)}\sim\sqrt{\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} }\:\sim\mathrm{1}−{x}^{\mathrm{2}} \\ $$$${tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\sim\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:\Rightarrow \\ $$$${f}\left({x}\right)\:\sim\frac{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}+{x}^{\mathrm{2}} }{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\:\mathrm{4}.\frac{\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\:=\mathrm{6}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right)=\mathrm{6} \\ $$$$ \\ $$
Answered by bobhans last updated on 04/Oct/20
![lim_(x→0) (((1+xsin x)−(1−2sin^2 x))/(tan^2 ((1/2)x))) ×lim_(x→0) (1/( (√(1+xsin x))+(√(cos 2x)))) = lim_(x→0) ((xsin x+2sin^2 x)/(tan^2 ((1/2)x))) × (1/2) = (1/2)×lim_(x→0) (([((x sin x)/x^2 ) +((2 sin^2 x)/x^2 )])/( [((tan^2 ((1/2)x))/x^2 )])) = (1/2)×(3/(((1/4))))= 6.](https://www.tinkutara.com/question/Q116424.png)
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\mathrm{xsin}\:\mathrm{x}\right)−\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)}\:×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{xsin}\:\mathrm{x}}+\sqrt{\mathrm{cos}\:\mathrm{2x}}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{xsin}\:\mathrm{x}+\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)}\:×\:\frac{\mathrm{1}}{\mathrm{2}}\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left[\frac{\mathrm{x}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} }\:+\frac{\mathrm{2}\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} }\right]}{\:\left[\frac{\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} }\right]}\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3}}{\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}=\:\mathrm{6}. \\ $$
