Question Number 48829 by Ali Yousafzai last updated on 29/Nov/18
![lim_(x→0) ((∫1^x [t^2 (e^(1/t) −1)−t]dt)/(x^2 ln (1+1/x)))](https://www.tinkutara.com/question/Q48829.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\int\mathrm{1}^{{x}} \left[{t}^{\mathrm{2}} \left({e}^{\mathrm{1}/{t}} −\mathrm{1}\right)−{t}\right]{dt}}{{x}^{\mathrm{2}} \mathrm{ln}\:\left(\mathrm{1}+\mathrm{1}/{x}\right)} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 29/Nov/18
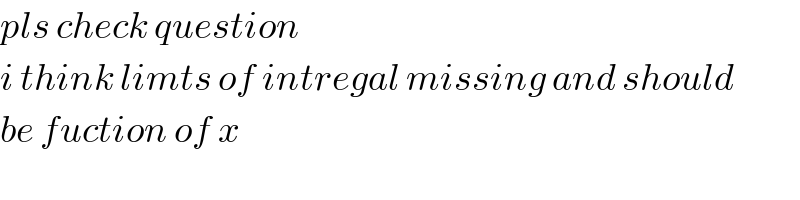
$${pls}\:{check}\:{question} \\ $$$${i}\:{think}\:{limts}\:{of}\:{intregal}\:{missing}\:{and}\:{should} \\ $$$${be}\:{fuction}\:{of}\:{x} \\ $$
Commented by Ali Yousafzai last updated on 29/Nov/18
The limit is for integral and I also think the problem is either wrong or something is missing. But it was sent to me by someone to solve. I asked also to clarify but he couldn't. So I put it forward for consideration of the forum.
Commented by maxmathsup by imad last updated on 29/Nov/18
![perhaps the question is find lim_(x→0) ∫_0 ^x (([t^2 (e^(1/t) −t])/(t^2 ln(1+(1/t))))dt...](https://www.tinkutara.com/question/Q48882.png)
$${perhaps}\:{the}\:{question}\:{is}\:{find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\int_{\mathrm{0}} ^{{x}} \:\:\:\:\frac{\left[{t}^{\mathrm{2}} \left({e}^{\frac{\mathrm{1}}{{t}}} −{t}\right]\right.}{{t}^{\mathrm{2}} {ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{t}}\right)}{dt}… \\ $$
