Question Number 26363 by d.monhbayr@gmail.com last updated on 24/Dec/17
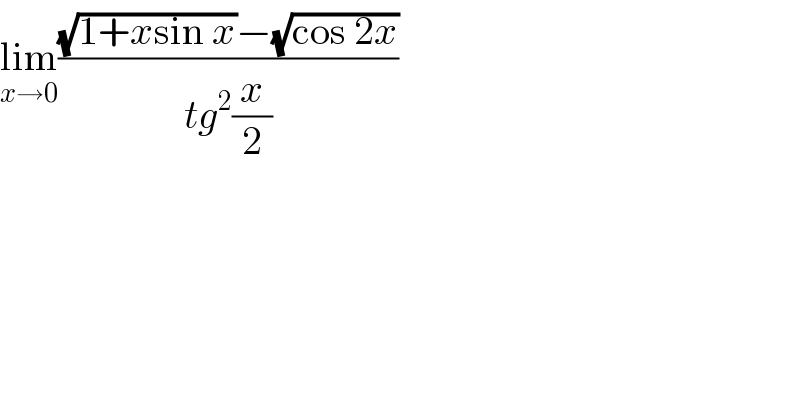
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{1}+{x}\mathrm{sin}\:{x}}−\sqrt{\mathrm{cos}\:\mathrm{2}{x}}}{{tg}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}} \\ $$
Commented by kaivan.ahmadi last updated on 24/Dec/17
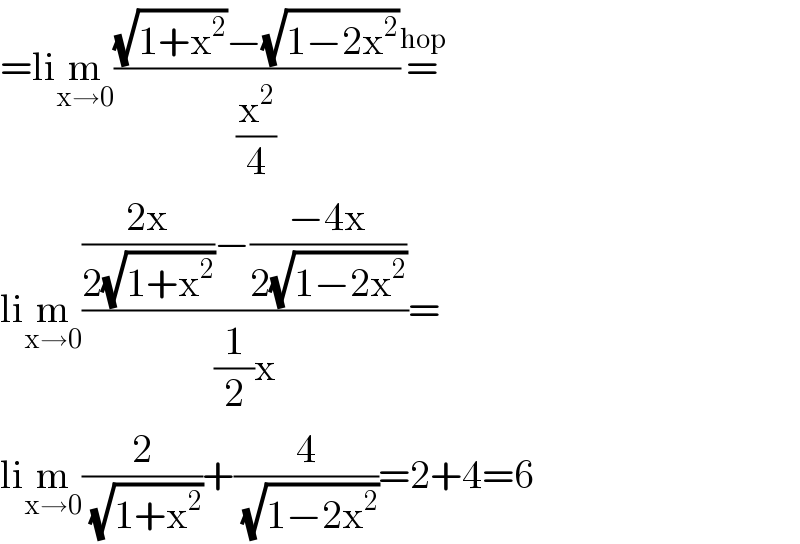
$$=\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{m}}\frac{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }−\sqrt{\mathrm{1}−\mathrm{2x}^{\mathrm{2}} }}{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}}\overset{\mathrm{hop}} {=} \\ $$$$\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{m}}\frac{\frac{\mathrm{2x}}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}−\frac{−\mathrm{4x}}{\mathrm{2}\sqrt{\mathrm{1}−\mathrm{2x}^{\mathrm{2}} }}}{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}}= \\ $$$$\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{m}}\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}+\frac{\mathrm{4}}{\:\sqrt{\mathrm{1}−\mathrm{2x}^{\mathrm{2}} }}=\mathrm{2}+\mathrm{4}=\mathrm{6} \\ $$
