Question Number 108265 by Study last updated on 15/Aug/20
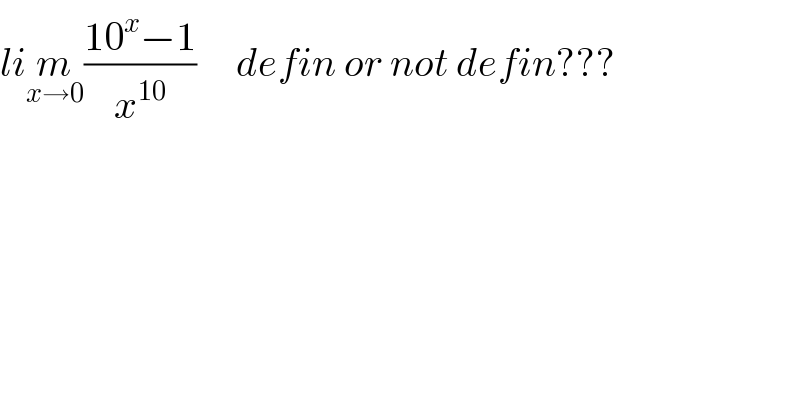
$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{\mathrm{10}^{{x}} −\mathrm{1}}{{x}^{\mathrm{10}} }\:\:\:\:\:{defin}\:{or}\:{not}\:{defin}??? \\ $$
Commented by Dwaipayan Shikari last updated on 15/Aug/20
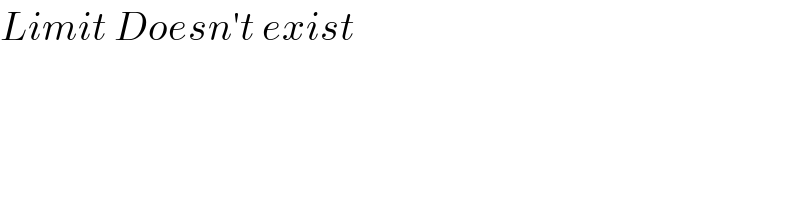
$${Limit}\:{Doesn}'{t}\:{exist} \\ $$
Answered by mathmax by abdo last updated on 15/Aug/20
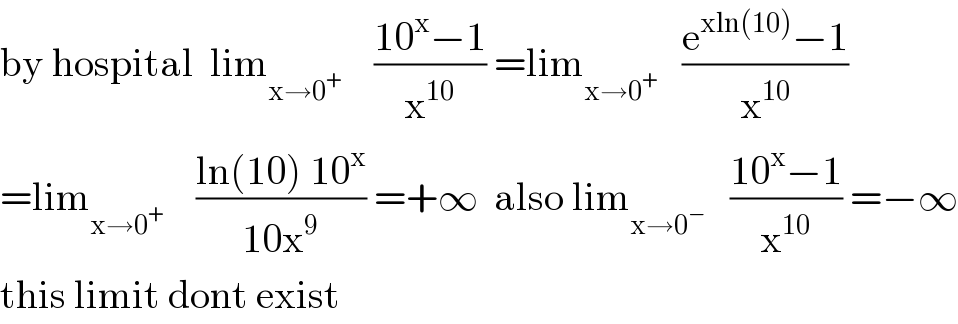
$$\mathrm{by}\:\mathrm{hospital}\:\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\:\:\frac{\mathrm{10}^{\mathrm{x}} −\mathrm{1}}{\mathrm{x}^{\mathrm{10}} }\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\:\frac{\mathrm{e}^{\mathrm{xln}\left(\mathrm{10}\right)} −\mathrm{1}}{\mathrm{x}^{\mathrm{10}} } \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\:\:\frac{\mathrm{ln}\left(\mathrm{10}\right)\:\mathrm{10}^{\mathrm{x}} }{\mathrm{10x}^{\mathrm{9}} }\:=+\infty\:\:\mathrm{also}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{−} } \:\:\:\frac{\mathrm{10}^{\mathrm{x}} −\mathrm{1}}{\mathrm{x}^{\mathrm{10}} }\:=−\infty \\ $$$$\mathrm{this}\:\mathrm{limit}\:\mathrm{dont}\:\mathrm{exist} \\ $$
