Question Number 86031 by arcana last updated on 26/Mar/20
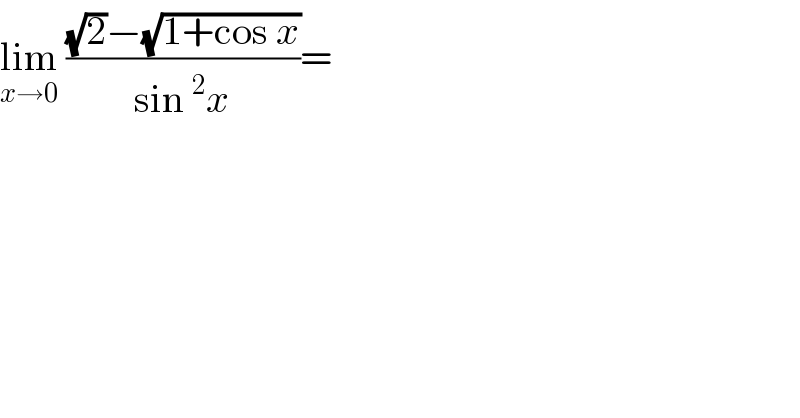
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}}{\mathrm{sin}\:^{\mathrm{2}} {x}}= \\ $$
Commented by arcana last updated on 26/Mar/20

$${the}\:{answer}\:{is}\:\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$
Commented by mathmax by abdo last updated on 26/Mar/20

$${i}\:{dont}\:{think}\:\:{chow}\:{your}\:{work}… \\ $$
Commented by abdomathmax last updated on 27/Mar/20
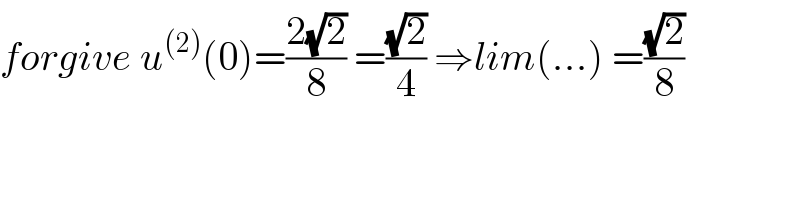
$${forgive}\:{u}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{8}}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\:\Rightarrow{lim}\left(…\right)\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}} \\ $$
Commented by john santu last updated on 26/Mar/20

$${not}\:{correct} \\ $$
Commented by abdomathmax last updated on 27/Mar/20

$${let}\:{verify}\:{by}\:{hospital}\:\:{theorem} \\ $$$${u}\left({x}\right)=\sqrt{\mathrm{2}}−\sqrt{\mathrm{1}+{cosx}}\:\Rightarrow{u}^{'} \left({x}\right)=\frac{{sinx}}{\mathrm{2}\sqrt{\mathrm{1}+{cosx}}} \\ $$$${u}^{\left(\mathrm{2}\right)} \left({x}\right)=\frac{\mathrm{2}{cosx}\sqrt{\mathrm{1}+{cosx}}\:−{sinx}\:×\frac{−{sinx}}{\:\sqrt{\mathrm{1}+{cosx}}}}{\mathrm{4}\left(\mathrm{1}+{cosx}\right)}\:\Rightarrow \\ $$$${u}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\:=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$${v}\left({x}\right)={sin}^{\mathrm{2}} {x}\:\Rightarrow{v}^{'} \left({x}\right)=\mathrm{2}{sinx}\:{cosx}\:{and} \\ $$$${v}^{\left(\mathrm{2}\right)} \left({x}\right)\:=\mathrm{2}{cos}^{\mathrm{2}} {x}\:−\mathrm{2}{sin}^{\mathrm{2}} {x}\:\Rightarrow{v}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\:=\mathrm{2}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{1}+{cosx}}}{{sin}^{\mathrm{2}} {x}}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$
Commented by arcana last updated on 27/Mar/20
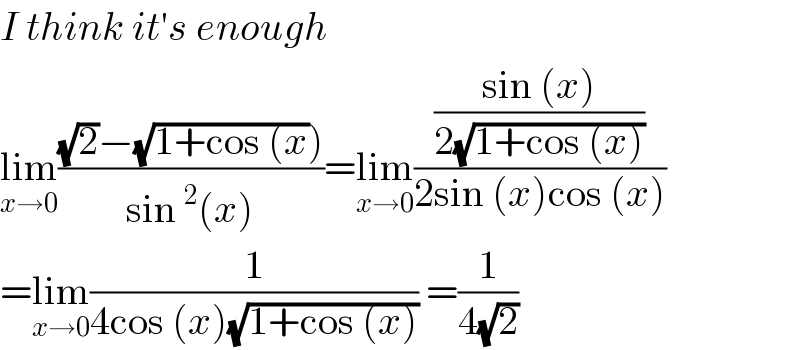
$${I}\:{think}\:{it}'{s}\:{enough} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left.\sqrt{\mathrm{2}}−\sqrt{\mathrm{1}+\mathrm{cos}\:\left({x}\right.}\right)}{\mathrm{sin}\:^{\mathrm{2}} \left({x}\right)}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{sin}\:\left({x}\right)}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{cos}\:\left({x}\right)}}}{\mathrm{2sin}\:\left({x}\right)\mathrm{cos}\:\left({x}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{4cos}\:\left({x}\right)\sqrt{\mathrm{1}+\mathrm{cos}\:\left({x}\right)}}\:=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$
Answered by john santu last updated on 26/Mar/20
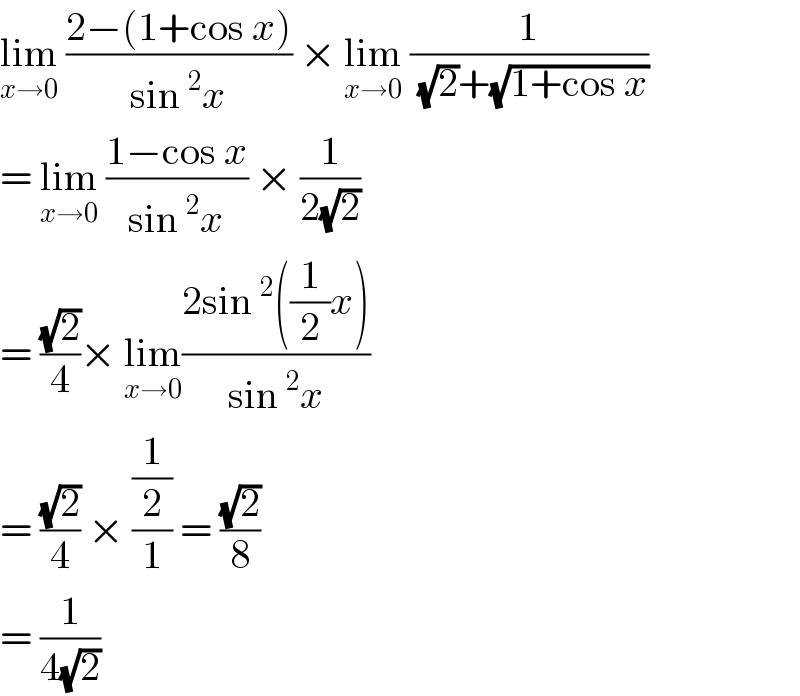
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}−\left(\mathrm{1}+\mathrm{cos}\:{x}\right)}{\mathrm{sin}\:^{\mathrm{2}} {x}}\:×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}+\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:{x}}{\mathrm{sin}\:^{\mathrm{2}} {x}}\:×\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}{x}\right)}{\mathrm{sin}\:^{\mathrm{2}} {x}} \\ $$$$=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\:×\:\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}}\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{8}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$
Commented by arcana last updated on 27/Mar/20
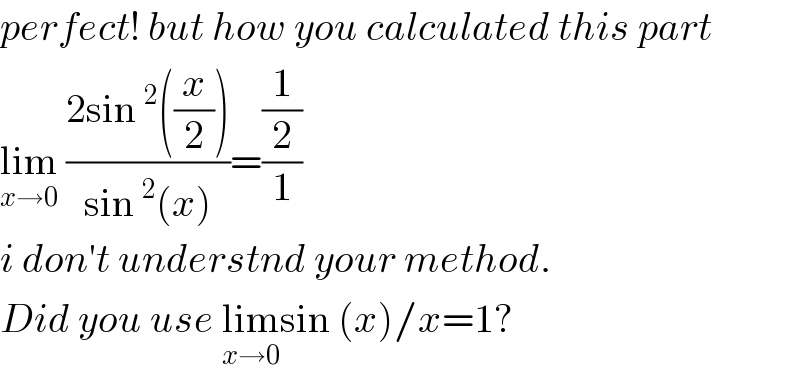
$${perfect}!\:{but}\:{how}\:{you}\:{calculated}\:{this}\:{part} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{sin}\:^{\mathrm{2}} \left({x}\right)}=\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}} \\ $$$${i}\:{don}'{t}\:{understnd}\:{your}\:{method}. \\ $$$${Did}\:{you}\:{use}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}sin}\:\left({x}\right)/{x}=\mathrm{1}? \\ $$
Commented by john santu last updated on 27/Mar/20

$${yes}. \\ $$$$ \\ $$
