Question Number 105114 by john santu last updated on 26/Jul/20
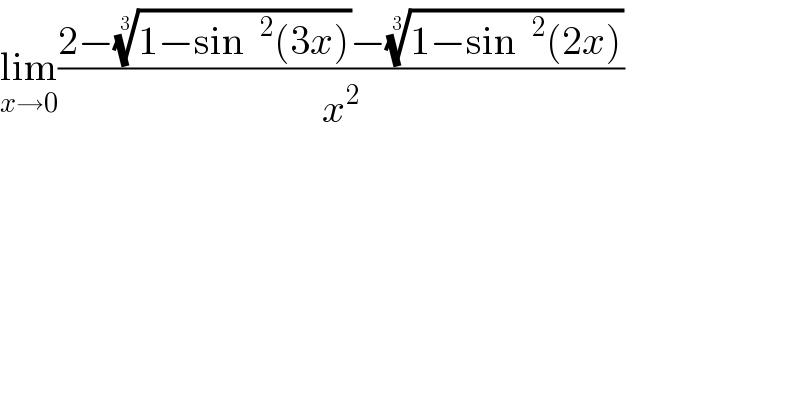
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}−\sqrt[{\mathrm{3}}]{\mathrm{1}−\mathrm{sin}\:\:^{\mathrm{2}} \left(\mathrm{3}{x}\right)}−\sqrt[{\mathrm{3}}]{\mathrm{1}−\mathrm{sin}\:\:^{\mathrm{2}} \left(\mathrm{2}{x}\right)}}{{x}^{\mathrm{2}} } \\ $$
Answered by bemath last updated on 26/Jul/20
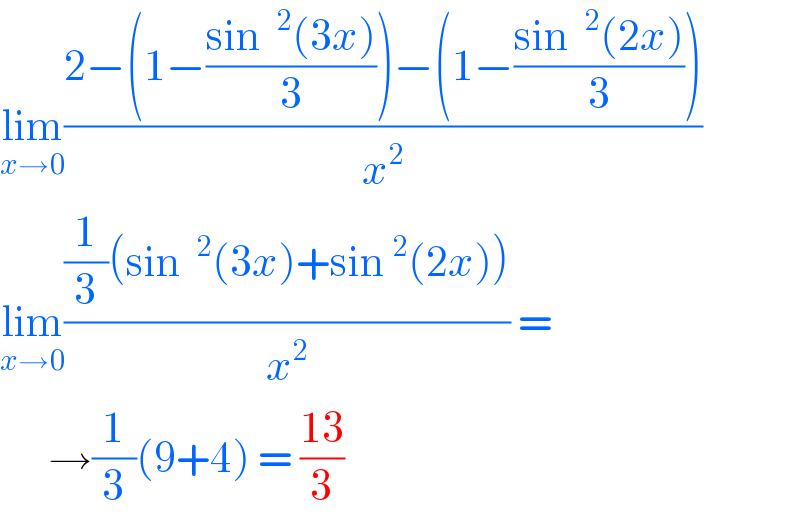
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}−\left(\mathrm{1}−\frac{\mathrm{sin}\:\:^{\mathrm{2}} \left(\mathrm{3}{x}\right)}{\mathrm{3}}\right)−\left(\mathrm{1}−\frac{\mathrm{sin}\:\:^{\mathrm{2}} \left(\mathrm{2}{x}\right)}{\mathrm{3}}\right)}{{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{sin}\:\:^{\mathrm{2}} \left(\mathrm{3}{x}\right)+\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{2}{x}\right)\right)}{{x}^{\mathrm{2}} }\:= \\ $$$$\:\:\:\:\:\:\rightarrow\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{9}+\mathrm{4}\right)\:=\:\frac{\mathrm{13}}{\mathrm{3}} \\ $$
Answered by OlafThorendsen last updated on 26/Jul/20
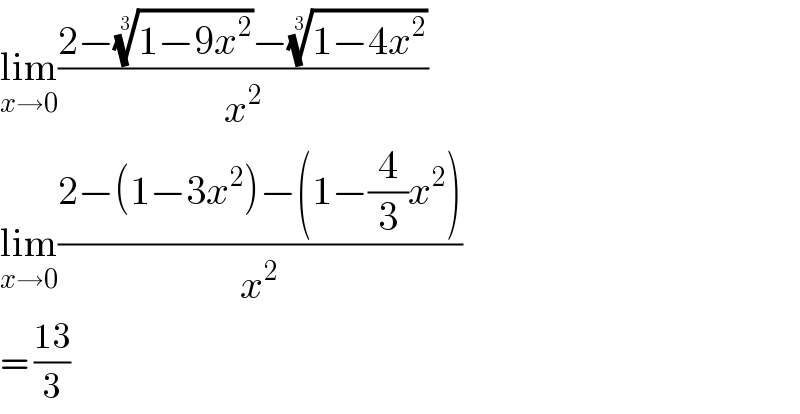
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}−\sqrt[{\mathrm{3}}]{\mathrm{1}−\mathrm{9}{x}^{\mathrm{2}} }−\sqrt[{\mathrm{3}}]{\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}−\left(\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} \right)−\left(\mathrm{1}−\frac{\mathrm{4}}{\mathrm{3}}{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{13}}{\mathrm{3}} \\ $$
