Question Number 121822 by liberty last updated on 12/Nov/20
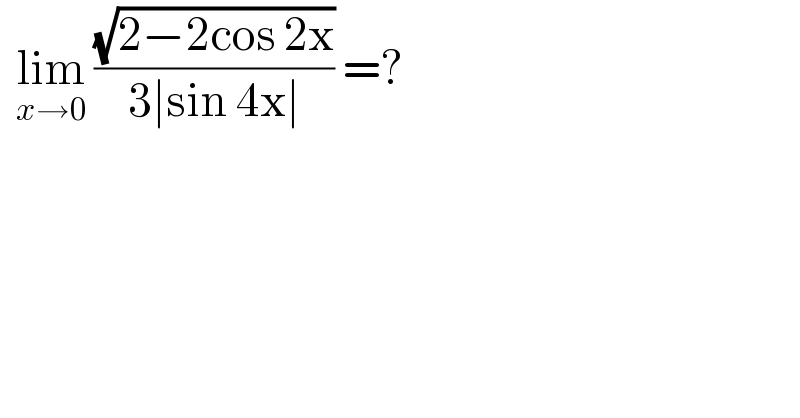
$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}−\mathrm{2cos}\:\mathrm{2x}}}{\mathrm{3}\mid\mathrm{sin}\:\mathrm{4x}\mid}\:=? \\ $$
Answered by bemath last updated on 12/Nov/20
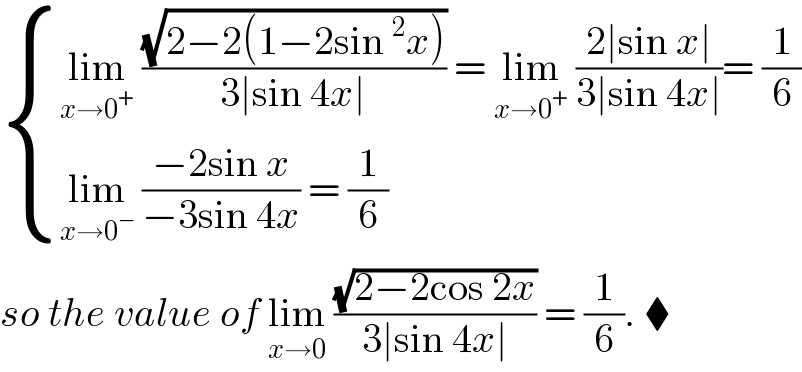
$$\begin{cases}{\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}−\mathrm{2}\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}\right)}}{\mathrm{3}\mid\mathrm{sin}\:\mathrm{4}{x}\mid}\:=\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{2}\mid\mathrm{sin}\:{x}\mid}{\mathrm{3}\mid\mathrm{sin}\:\mathrm{4}{x}\mid}=\:\frac{\mathrm{1}}{\mathrm{6}}}\\{\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\frac{−\mathrm{2sin}\:{x}}{−\mathrm{3sin}\:\mathrm{4}{x}}\:=\:\frac{\mathrm{1}}{\mathrm{6}}}\end{cases} \\ $$$${so}\:{the}\:{value}\:{of}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}−\mathrm{2cos}\:\mathrm{2}{x}}}{\mathrm{3}\mid\mathrm{sin}\:\mathrm{4}{x}\mid}\:=\:\frac{\mathrm{1}}{\mathrm{6}}.\:\blacklozenge \\ $$
