Menu Close

lim-x-0-2-3-x-1-4x-2-

Tinku Tara 0 Comments
Pin




Question Number 107030 by bemath last updated on 08/Aug/20
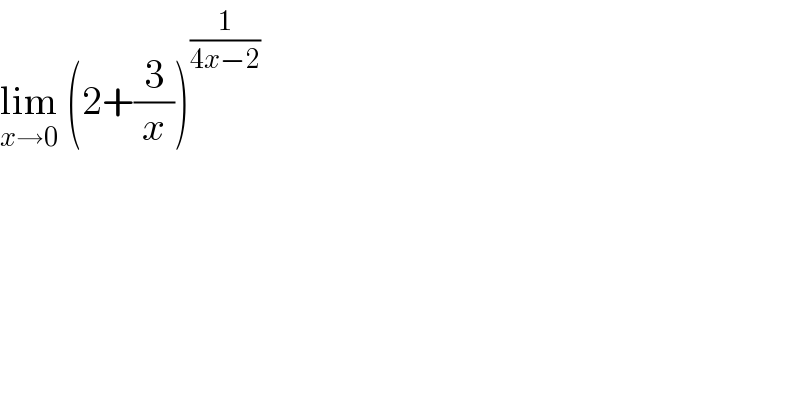
lim_(x→0) (2+(3/x))^(1/(4x−2))
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{2}+\frac{\mathrm{3}}{{x}}\right)^{\frac{\mathrm{1}}{\mathrm{4}{x}−\mathrm{2}}} \\ $$
Commented by kaivan.ahmadi last updated on 08/Aug/20
y=(2+(3/x))^(1/(4x−2)) ⇒lim_(x→∞) lny=lim_(x→∞) ((ln(2+(3/x)))/(4x−2))∼ lim_(x→∞) ((−3)/(4x^2 (2+(3/x))))=0⇒lim_(x→∞) y=e^0 =1
$${y}=\left(\mathrm{2}+\frac{\mathrm{3}}{{x}}\right)^{\frac{\mathrm{1}}{\mathrm{4}{x}−\mathrm{2}}} \Rightarrow{lim}_{{x}\rightarrow\infty} {lny}={lim}_{{x}\rightarrow\infty} \frac{{ln}\left(\mathrm{2}+\frac{\mathrm{3}}{{x}}\right)}{\mathrm{4}{x}−\mathrm{2}}\sim \\ $$$${lim}_{{x}\rightarrow\infty} \frac{−\mathrm{3}}{\mathrm{4}{x}^{\mathrm{2}} \left(\mathrm{2}+\frac{\mathrm{3}}{{x}}\right)}=\mathrm{0}\Rightarrow{lim}_{{x}\rightarrow\infty} {y}={e}^{\mathrm{0}} =\mathrm{1} \\ $$
Answered by Dwaipayan Shikari last updated on 08/Aug/20
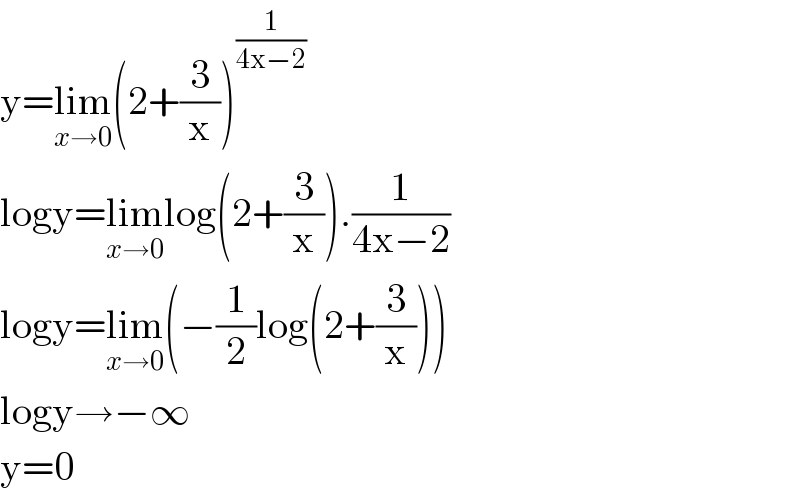
y=lim_(x→0) (2+(3/x))^(1/(4x−2)) logy=lim_(x→0) log(2+(3/x)).(1/(4x−2)) logy=lim_(x→0) (−(1/2)log(2+(3/x))) logy→−∞ y=0
$$\mathrm{y}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{2}+\frac{\mathrm{3}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{4x}−\mathrm{2}}} \\ $$$$\mathrm{logy}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}log}\left(\mathrm{2}+\frac{\mathrm{3}}{\mathrm{x}}\right).\frac{\mathrm{1}}{\mathrm{4x}−\mathrm{2}} \\ $$$$\mathrm{logy}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\mathrm{2}+\frac{\mathrm{3}}{\mathrm{x}}\right)\right) \\ $$$$\mathrm{logy}\rightarrow−\infty \\ $$$$\mathrm{y}=\mathrm{0} \\ $$
Commented by bemath last updated on 08/Aug/20
not correct sir
$${not}\:{correct}\:{sir} \\ $$
Commented by Dwaipayan Shikari last updated on 08/Aug/20
Commented by bemath last updated on 08/Aug/20
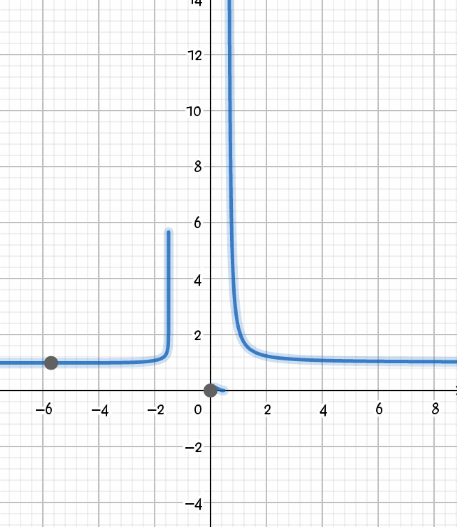
Answered by john santu last updated on 08/Aug/20
@JS@ we have formula lim_(x→0) (1+x)^(1/x) = e lim_(x→0) (1+(((x+3)/x)))^(1/(4x−2)) = lim_(x→0) [(1+(((x+3)/x)))^(((x/(x+3)))) ]^((x+3)/(x(4x−2))) = e^(lim_(x→0 ) (((x+3)/(4x^2 −2x)))) = e^∞ = ∞
$$\:\:\:\:\:\:@\mathrm{JS}@ \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{formula}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\mathrm{x}\right)^{\frac{\mathrm{1}}{\mathrm{x}}} =\:\mathrm{e} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\left(\frac{\mathrm{x}+\mathrm{3}}{\mathrm{x}}\right)\right)^{\frac{\mathrm{1}}{\mathrm{4x}−\mathrm{2}}} =\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\mathrm{1}+\left(\frac{\mathrm{x}+\mathrm{3}}{\mathrm{x}}\right)\right)^{\left(\frac{\mathrm{x}}{\mathrm{x}+\mathrm{3}}\right)} \right]^{\frac{\mathrm{x}+\mathrm{3}}{\mathrm{x}\left(\mathrm{4x}−\mathrm{2}\right)}} \\ $$$$=\:\mathrm{e}\:^{\underset{{x}\rightarrow\mathrm{0}\:} {\mathrm{lim}}\left(\frac{\mathrm{x}+\mathrm{3}}{\mathrm{4x}^{\mathrm{2}} −\mathrm{2x}}\right)} =\:\mathrm{e}^{\infty} \:=\:\infty\: \\ $$
Commented by bemath last updated on 08/Aug/20
thank you
$${thank}\:{you} \\ $$
Answered by bemath last updated on 08/Aug/20
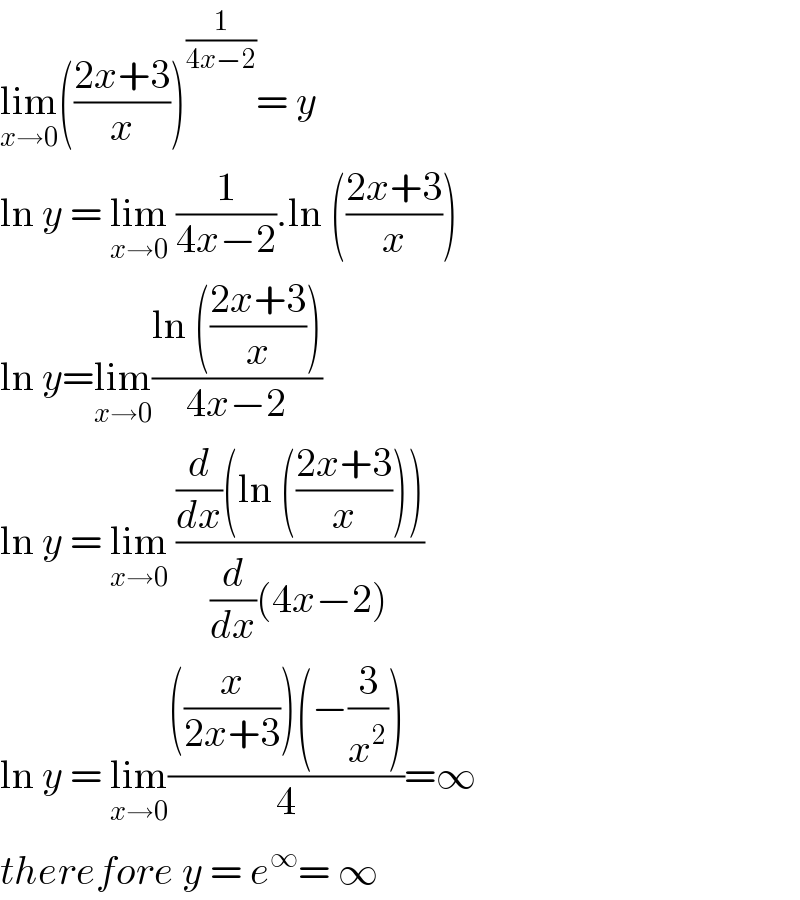
lim_(x→0) (((2x+3)/x))^(1/(4x−2)) = y ln y = lim_(x→0) (1/(4x−2)).ln (((2x+3)/x)) ln y=lim_(x→0) ((ln (((2x+3)/x)))/(4x−2)) ln y = lim_(x→0) (((d/dx)(ln (((2x+3)/x))))/((d/dx)(4x−2))) ln y = lim_(x→0) ((((x/(2x+3)))(−(3/x^2 )))/4)=∞ therefore y = e^∞ = ∞
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2}{x}+\mathrm{3}}{{x}}\right)^{\frac{\mathrm{1}}{\mathrm{4}{x}−\mathrm{2}}} =\:{y} \\ $$$$\mathrm{ln}\:{y}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{4}{x}−\mathrm{2}}.\mathrm{ln}\:\left(\frac{\mathrm{2}{x}+\mathrm{3}}{{x}}\right) \\ $$$$\mathrm{ln}\:{y}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\:\left(\frac{\mathrm{2}{x}+\mathrm{3}}{{x}}\right)}{\mathrm{4}{x}−\mathrm{2}} \\ $$$$\mathrm{ln}\:{y}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{d}}{{dx}}\left(\mathrm{ln}\:\left(\frac{\mathrm{2}{x}+\mathrm{3}}{{x}}\right)\right)}{\frac{{d}}{{dx}}\left(\mathrm{4}{x}−\mathrm{2}\right)} \\ $$$$\mathrm{ln}\:{y}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{{x}}{\mathrm{2}{x}+\mathrm{3}}\right)\left(−\frac{\mathrm{3}}{{x}^{\mathrm{2}} }\right)}{\mathrm{4}}=\infty \\ $$$${therefore}\:{y}\:=\:{e}^{\infty} =\:\infty \\ $$
Commented by Dwaipayan Shikari last updated on 08/Aug/20
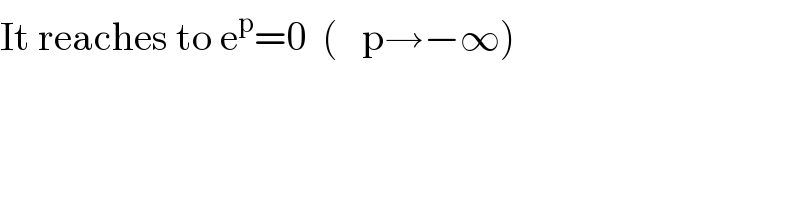
It reaches to e^p =0 ( p→−∞)
$$\mathrm{It}\:\mathrm{reaches}\:\mathrm{to}\:\mathrm{e}^{\mathrm{p}} =\mathrm{0}\:\:\left(\:\:\:\mathrm{p}\rightarrow−\infty\right) \\ $$
Answered by mathmax by abdo last updated on 08/Aug/20
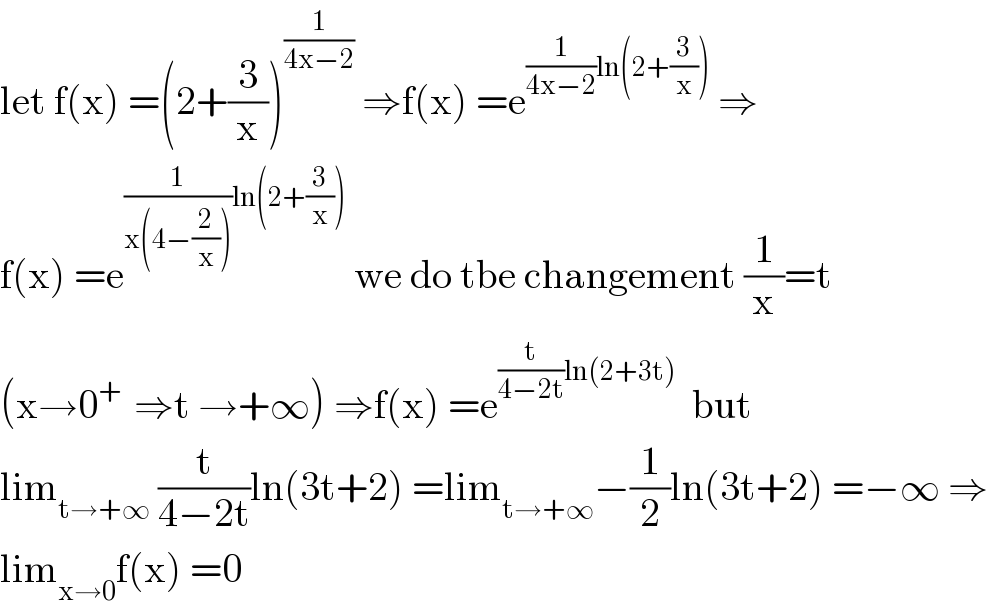
let f(x) =(2+(3/x))^(1/(4x−2)) ⇒f(x) =e^((1/(4x−2))ln(2+(3/x))) ⇒ f(x) =e^((1/(x(4−(2/x))))ln(2+(3/x))) we do tbe changement (1/x)=t (x→0^(+ ) ⇒t →+∞) ⇒f(x) =e^((t/(4−2t))ln(2+3t)) but lim_(t→+∞) (t/(4−2t))ln(3t+2) =lim_(t→+∞) −(1/2)ln(3t+2) =−∞ ⇒ lim_(x→0) f(x) =0
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\left(\mathrm{2}+\frac{\mathrm{3}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{4x}−\mathrm{2}}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{4x}−\mathrm{2}}\mathrm{ln}\left(\mathrm{2}+\frac{\mathrm{3}}{\mathrm{x}}\right)} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{4}−\frac{\mathrm{2}}{\mathrm{x}}\right)}\mathrm{ln}\left(\mathrm{2}+\frac{\mathrm{3}}{\mathrm{x}}\right)} \:\mathrm{we}\:\mathrm{do}\:\mathrm{tbe}\:\mathrm{changement}\:\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{t}\: \\ $$$$\left(\mathrm{x}\rightarrow\mathrm{0}^{+\:} \:\Rightarrow\mathrm{t}\:\rightarrow+\infty\right)\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\mathrm{t}}{\mathrm{4}−\mathrm{2t}}\mathrm{ln}\left(\mathrm{2}+\mathrm{3t}\right)} \:\:\mathrm{but} \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \:\frac{\mathrm{t}}{\mathrm{4}−\mathrm{2t}}\mathrm{ln}\left(\mathrm{3t}+\mathrm{2}\right)\:=\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{3t}+\mathrm{2}\right)\:=−\infty\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *