Question Number 127002 by bramlexs22 last updated on 26/Dec/20
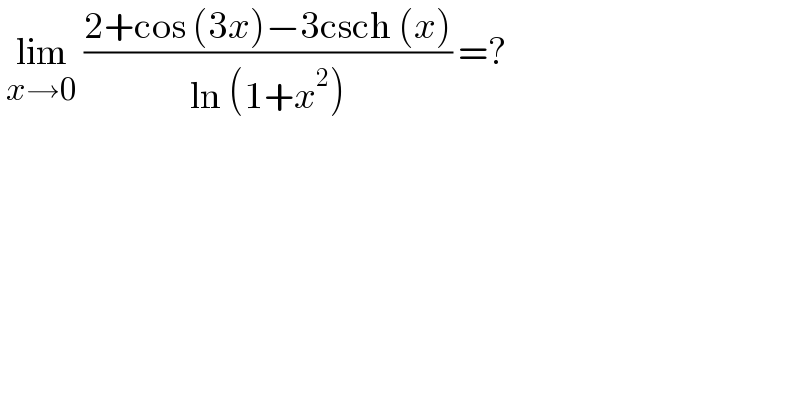
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}+\mathrm{cos}\:\left(\mathrm{3}{x}\right)−\mathrm{3csch}\:\left({x}\right)}{\mathrm{ln}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:=? \\ $$
Commented by Evimene last updated on 26/Dec/20

$$ \\ $$$$\:\: \\ $$$$\mathrm{add}\:\mathrm{me}\:\mathrm{on}\:\mathrm{facebook} \\ $$$$\mathrm{on}\:\mathrm{cadet}\:\mathrm{paise}\:\mathrm{maldonna}\:\mathrm{just}\:\mathrm{not}\:\mathrm{used}\:\mathrm{to} \\ $$$$\mathrm{it}\:\mathrm{here}\:\mathrm{my}\:\mathrm{data}\:\mathrm{will}\:\mathrm{soon}\:\mathrm{finish} \\ $$
Answered by liberty last updated on 26/Dec/20
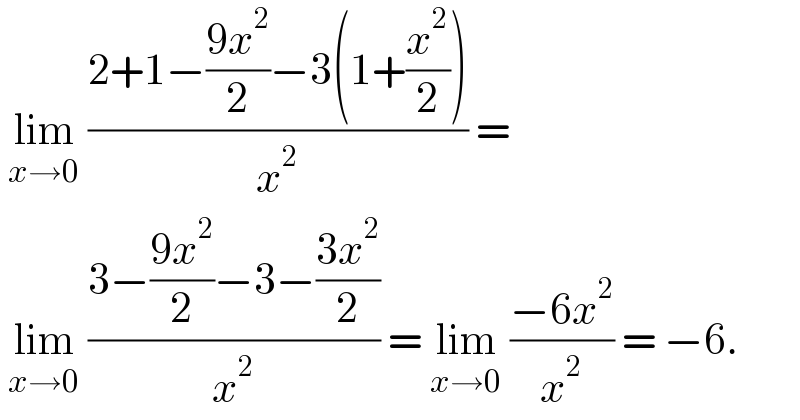
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}+\mathrm{1}−\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{3}\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)}{{x}^{\mathrm{2}} }\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3}−\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{3}−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}}{{x}^{\mathrm{2}} }\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{6}{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\:=\:−\mathrm{6}. \\ $$
