lim-x-0-2-sin-2-x-1-ln-cos-x-

Question Number 92741 by john santu last updated on 09/May/20

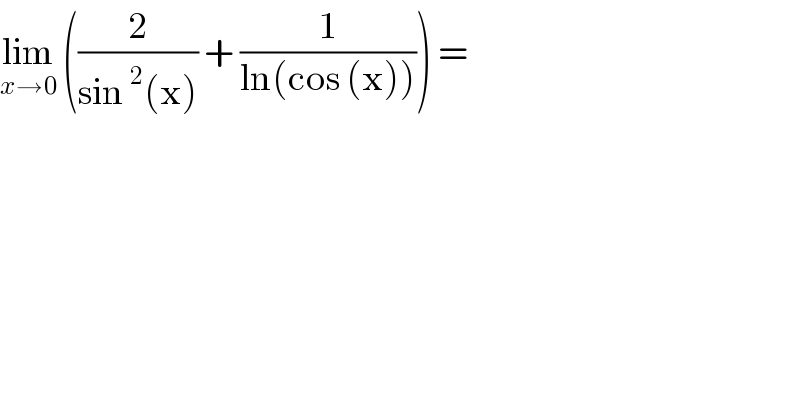
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{2}}{\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{x}\right)}\:+\:\frac{\mathrm{1}}{\mathrm{ln}\left(\mathrm{cos}\:\left(\mathrm{x}\right)\right)}\right)\:= \\ $$

Commented by abdomathmax last updated on 09/May/20

$${yes}\:{yes}\:…{i}\:{will}\:{delet}\:{the}\:{post}\:…{nevermind}… \\ $$

Commented by i jagooll last updated on 09/May/20

Commented by i jagooll last updated on 09/May/20

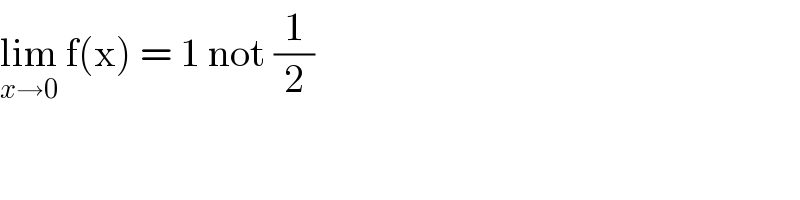
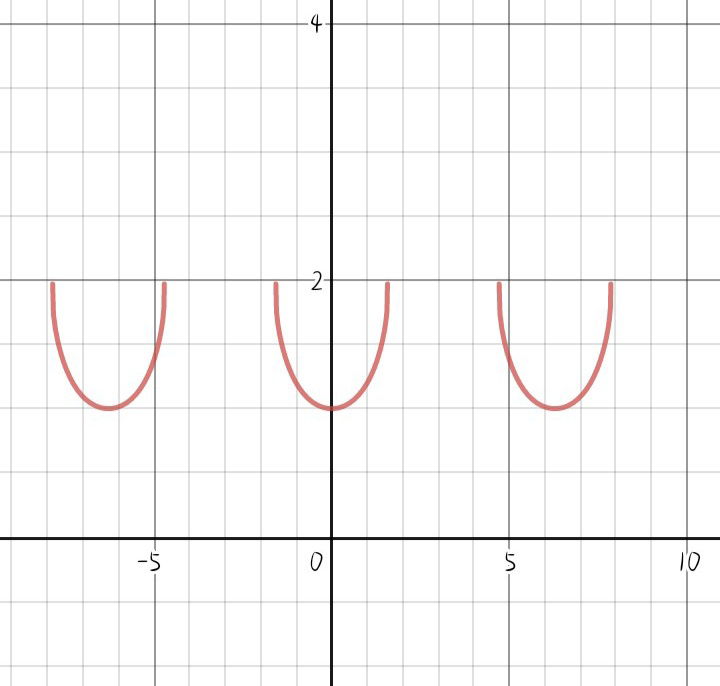
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{1}\:\mathrm{not}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by msup by abdo last updated on 09/May/20

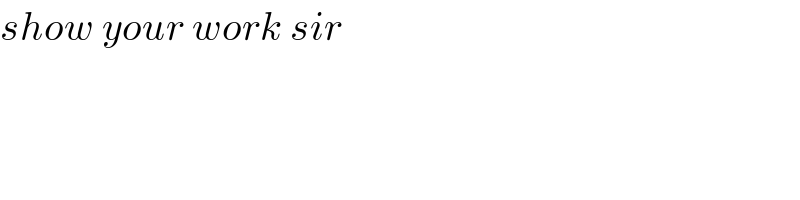
$${show}\:{your}\:{work}\:{sir} \\ $$

Commented by i jagooll last updated on 09/May/20

$$\mathrm{look}\:\mathrm{at}\:\mathrm{picture} \\ $$

Commented by john santu last updated on 09/May/20

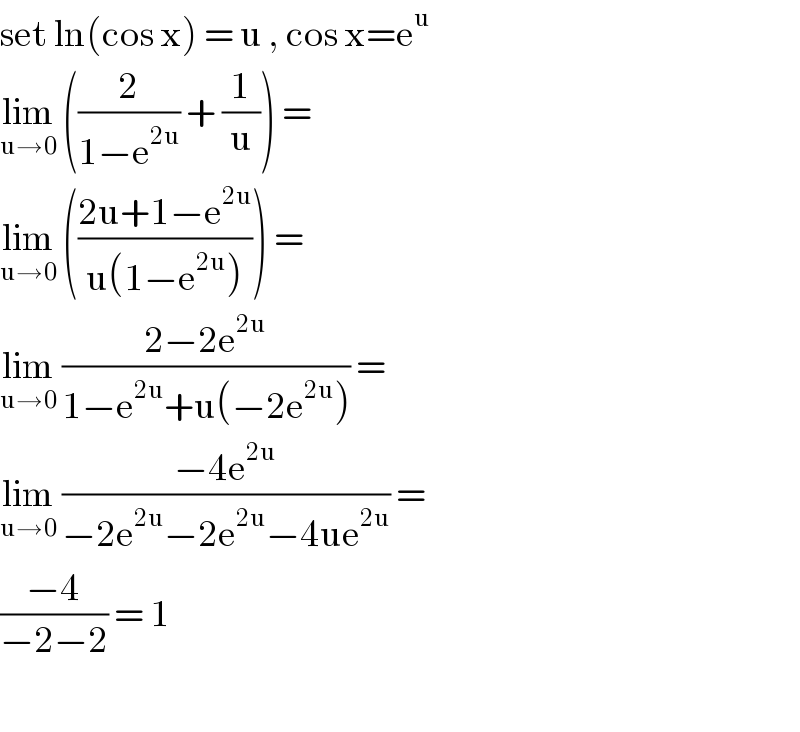
set ln(cos x) = u , cos x=e^u lim_(u→0) ((2/(1−e^(2u) )) + (1/u)) = lim_(u→0) (((2u+1−e^(2u) )/(u(1−e^(2u) )))) = lim_(u→0) ((2−2e^(2u) )/(1−e^(2u) +u(−2e^(2u) ))) = lim_(u→0) ((−4e^(2u) )/(−2e^(2u) −2e^(2u) −4ue^(2u) )) = ((−4)/(−2−2)) = 1

$$\mathrm{set}\:\mathrm{ln}\left(\mathrm{cos}\:\mathrm{x}\right)\:=\:\mathrm{u}\:,\:\mathrm{cos}\:\mathrm{x}=\mathrm{e}^{\mathrm{u}} \\ $$$$\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{2}}{\mathrm{1}−\mathrm{e}^{\mathrm{2u}} }\:+\:\frac{\mathrm{1}}{\mathrm{u}}\right)\:= \\ $$$$\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{2u}+\mathrm{1}−\mathrm{e}^{\mathrm{2u}} }{\mathrm{u}\left(\mathrm{1}−\mathrm{e}^{\mathrm{2u}} \right)}\right)\:= \\ $$$$\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}−\mathrm{2e}^{\mathrm{2u}} }{\mathrm{1}−\mathrm{e}^{\mathrm{2u}} +\mathrm{u}\left(−\mathrm{2e}^{\mathrm{2u}} \right)}\:= \\ $$$$\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{4e}^{\mathrm{2u}} }{−\mathrm{2e}^{\mathrm{2u}} −\mathrm{2e}^{\mathrm{2u}} −\mathrm{4ue}^{\mathrm{2u}} }\:= \\ $$$$\frac{−\mathrm{4}}{−\mathrm{2}−\mathrm{2}}\:=\:\mathrm{1} \\ $$$$ \\ $$

Commented by john santu last updated on 09/May/20

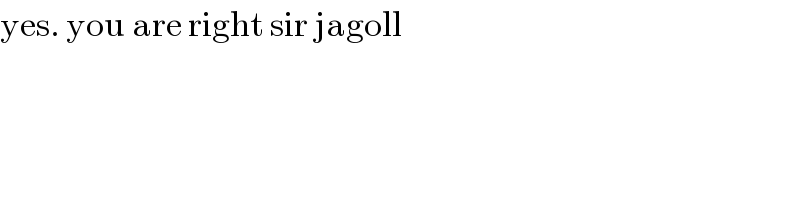
$$\mathrm{yes}.\:\mathrm{you}\:\mathrm{are}\:\mathrm{right}\:\mathrm{sir}\:\mathrm{jagoll} \\ $$

Commented by john santu last updated on 09/May/20

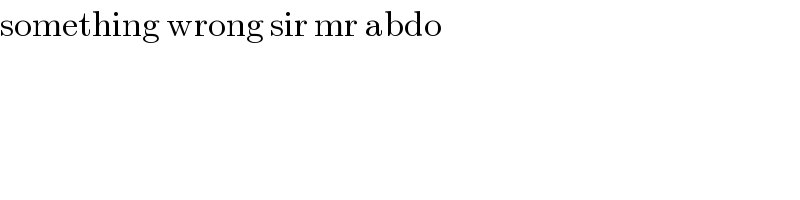
$$\mathrm{something}\:\mathrm{wrong}\:\mathrm{sir}\:\mathrm{mr}\:\mathrm{abdo} \\ $$

Commented by i jagooll last updated on 09/May/20

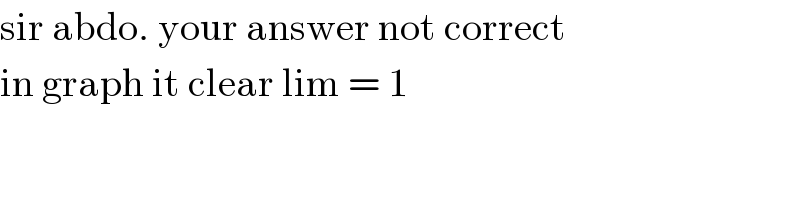
sir abdo. your answer not correct in graph it clear lim = 1

$$\mathrm{sir}\:\mathrm{abdo}.\:\mathrm{your}\:\mathrm{answer}\:\mathrm{not}\:\mathrm{correct} \\ $$$$\mathrm{in}\:\mathrm{graph}\:\mathrm{it}\:\mathrm{clear}\:\mathrm{lim}\:=\:\mathrm{1} \\ $$

Facebook Tweet Pin

lim-x-0-2-sin-2-x-1-ln-cos-x-

Leave a Reply Cancel reply