Question Number 184881 by mathlove last updated on 13/Jan/23
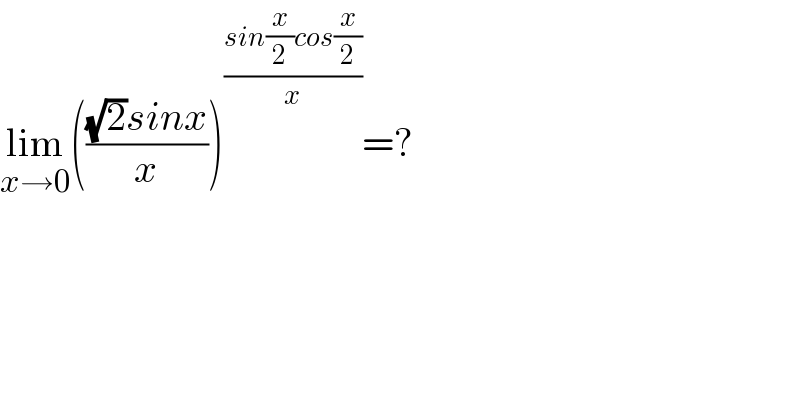
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\sqrt{\mathrm{2}}{sinx}}{{x}}\right)^{\frac{{sin}\frac{{x}}{\mathrm{2}}{cos}\frac{{x}}{\mathrm{2}}}{{x}}} =? \\ $$
Answered by aba last updated on 13/Jan/23
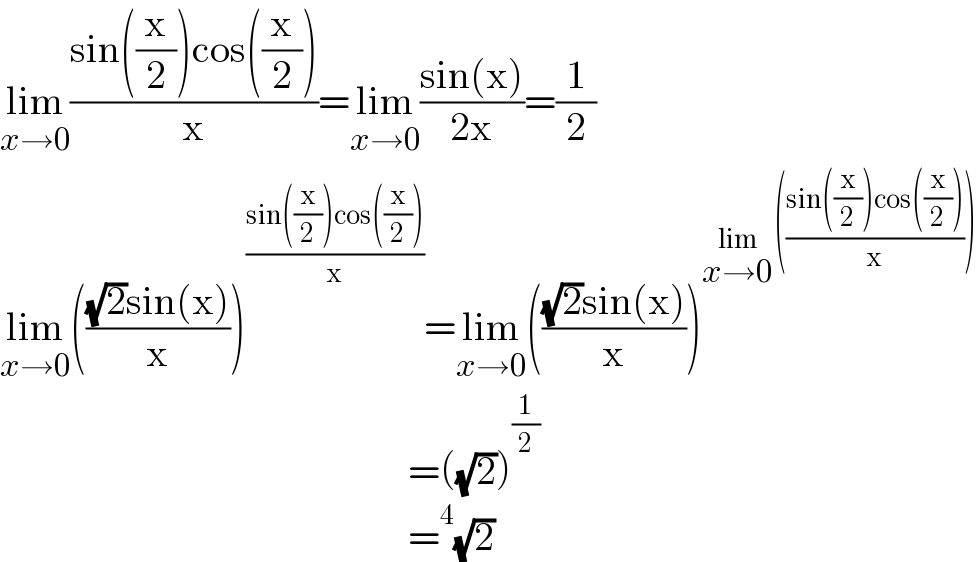
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)}{\mathrm{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{2x}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\sqrt{\mathrm{2}}\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{x}}\right)^{\frac{\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)}{\mathrm{x}}} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\sqrt{\mathrm{2}}\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{x}}\right)^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)}{\mathrm{x}}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\sqrt{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=^{\mathrm{4}} \sqrt{\mathrm{2}} \\ $$
