Question Number 91182 by jagoll last updated on 28/Apr/20
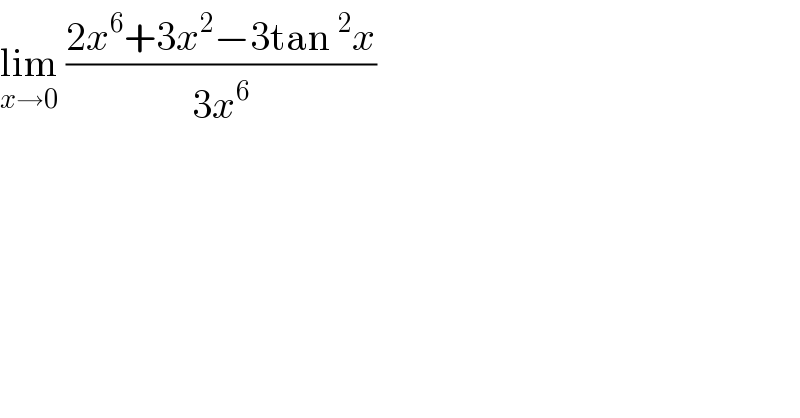
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}{x}^{\mathrm{6}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3tan}\:^{\mathrm{2}} {x}}{\mathrm{3}{x}^{\mathrm{6}} } \\ $$
Answered by john santu last updated on 28/Apr/20
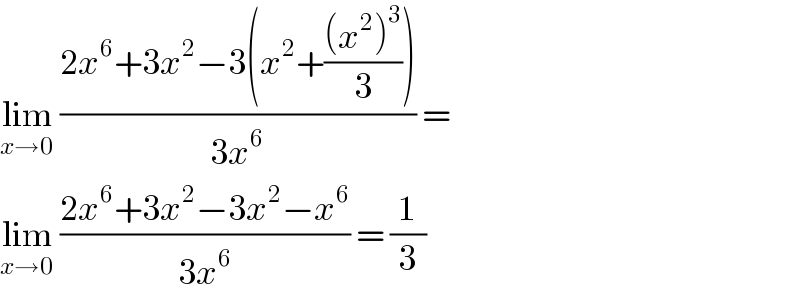
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}{x}^{\mathrm{6}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}\left({x}^{\mathrm{2}} +\frac{\left({x}^{\mathrm{2}} \right)^{\mathrm{3}} }{\mathrm{3}}\right)}{\mathrm{3}{x}^{\mathrm{6}} }\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}{x}^{\mathrm{6}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{x}^{\mathrm{2}} −{x}^{\mathrm{6}} }{\mathrm{3}{x}^{\mathrm{6}} }\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by jagoll last updated on 28/Apr/20
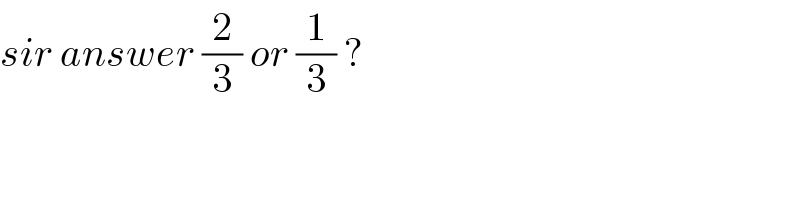
$${sir}\:{answer}\:\frac{\mathrm{2}}{\mathrm{3}}\:{or}\:\frac{\mathrm{1}}{\mathrm{3}}\:? \\ $$
Commented by MJS last updated on 28/Apr/20

$$\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{2}{x}^{\mathrm{6}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{x}^{\mathrm{2}} −{x}^{\mathrm{6}} \\ $$
Commented by jagoll last updated on 28/Apr/20
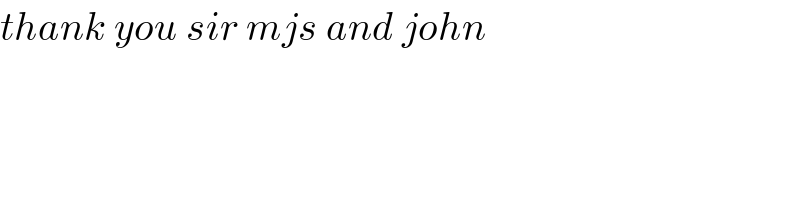
$${thank}\:{you}\:{sir}\:{mjs}\:{and}\:{john}\: \\ $$
